摘要:15.如图.在直三棱柱ABC-A1B1C1中. AB=BC=.BB1=2.. E.F分别为AA1.C1B1的中点.沿棱柱的表面从E 到F两点的最短路径的长度为 . [思路点拨]本题主要考查空间距离转化为平面距离. [正确解答]分别延将E.F展开到同一平面内.则易得:.,或 比较可得.最小值为. [解后反思]将平面图形空间化也是立体几何的另一种问题形式,在做立体几何中,许多问题都是空间图形进行平面化,努力将一个个空间图形,通过所学的几何知识,转化成平面图形,最后使用平面几何的若干知识解决,而本题却反其道而行之,所以在做法上就不能和上述的方法相同,但在本质上有许多相通之处,在这类题目中,尽量找出两者图形过程中的联系之处,哪些量变啦,哪些量没有变,然后解决起来,就会顺手多啦.
网址:http://m.1010jiajiao.com/timu3_id_4469163[举报]
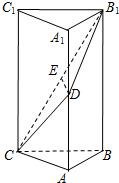 如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=1,AA1=2,D、E分别是AA1、B1C的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=1,AA1=2,D、E分别是AA1、B1C的中点.(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求异面直线A1C1与B1D所成角的大小;
(Ⅲ)求二面角C-B1D-B的大小. 查看习题详情和答案>>
 如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,P为A1C1的中点,AB=BC=kPA.
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,P为A1C1的中点,AB=BC=kPA.(I)求三棱锥P-AB1C与三棱锥C1-AB1P的体积之比;
(II)当k为何值时,直线PA⊥B1C. 查看习题详情和答案>>
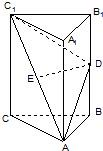 如图,在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点.(I)证明:ED为异面直线BB1与AC1的公垂线;
(II)设AA1=AC=
| 2 |
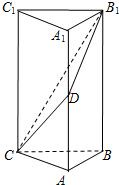 如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=1,AA1=2,D是AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=1,AA1=2,D是AA1的中点. 17、如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,点M是线段AB中点,N是线段A1C1的中点.
17、如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,点M是线段AB中点,N是线段A1C1的中点.