摘要:16.以下同个关于圆锥曲线的命题中 ①设A.B为两个定点.k为非零常数..则动点P的轨迹为双曲线, ②设定圆C上一定点A作圆的动点弦AB.O为坐标原点.若则动点P的轨迹为椭圆, ③方程的两根可分别作为椭圆和双曲线的离心率, ④双曲线有相同的焦点. 其中真命题的序号为 [思路点拨]本题主要考查圆锥曲线的定义和性质主要由a,b,c,e的关系求得 [正确解答]双曲线的第一定义是:平面上的动点P到两定点是A,B之间的距离的差的绝对值为常数2a,且,那么P点的轨迹为双曲线,故①错. 由,得P为弦AB的中点,故②错. 设的两根为则可知两根互与为倒数,且均为正,故③对. 的焦点坐标(),而的焦点坐标(),故④正确. [解后反思]要牢牢掌握椭圆,双曲线的第一定义,同时还要掌握圆锥曲线的统一定义,弄清圆锥曲线中a,b,c,e的相互关系.
网址:http://m.1010jiajiao.com/timu3_id_4469164[举报]
以下同个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,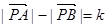 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动弦AB,O为坐标原点,若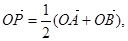 则动点P的轨迹为
则动点P的轨迹为
椭圆;
③方程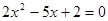 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
查看习题详情和答案>>
以下同个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,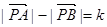 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动点弦AB,O为坐标原点,若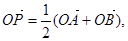 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③方程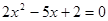 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
查看习题详情和答案>>
以下同个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,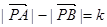 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动弦AB,O为坐标原点,若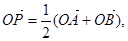 则动点P的轨迹为
则动点P的轨迹为
椭圆;
③方程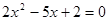 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
①设A、B为两个定点,k为非零常数,
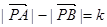 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;②过定圆C上一定点A作圆的动弦AB,O为坐标原点,若
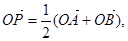 则动点P的轨迹为
则动点P的轨迹为椭圆;
③方程
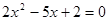 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;④双曲线
 有相同的焦点.
有相同的焦点.其中真命题的序号为 (写出所有真命题的序号)
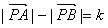 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线; 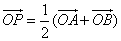 ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆; 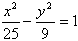 与椭圆
与椭圆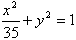 有相同的焦点。
有相同的焦点。