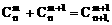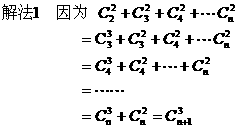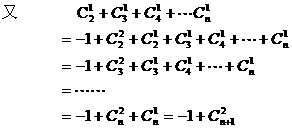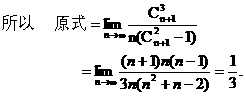20.A、B两个代表队进行乒乓球对抗赛,每队三名队员,A队队员是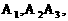 B队队员是
B队队员是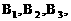 按以往多次比赛的统计,对阵队员之间胜负概率如下:
按以往多次比赛的统计,对阵队员之间胜负概率如下:
现按表中对阵方式出场,每场胜队得1分,负队得0分.设A队、B队最后所得总分分别为ξ、η.
|
对阵队员 |
A队队员胜的概率 |
A队队员负的概率 |
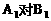 |
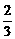 |
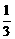 |
 |
 |
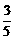 |
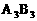 |
 |
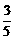 |
(Ⅰ)求ξ,η的概率分布;
(Ⅱ)求Eξ,Eη.
[命题意图] 本题主要考查离散型随机变量分布列和数学期望等概念与计算,以及运用概率知识认识和讨论实际问题的能力.
该题的取材贴近考生日常生活,以广大考生都熟悉的乒乓球比赛为素材,用列表的方式,给出对阵队员间胜负的概率,并规定每场胜负的得分规则.这样的条件下,赛后球队所得总分是离散型随机变量.本题要求考生计算该随机变量的分布列和数学期望.
这样设计试题,应用性强,也能贴近考生实际,符合《考试说明》的要求.
[解题思路] 为了求随机变量ξ和η的概率分布,必须先确定它们是离散型还是连续型.依题意,它们都是离散型随机变量,且满足ξ+η=3.所以只须求出ξ(或η)的概率分布,便可立即写出η(或ξ)的概率分布.
为了求ξ的概率分布,首先应弄清ξ可能取哪些值?这些值表示怎样的随机事件?进而应用随机事件概率计算公式(如乘法公式、加法公式等),求出ξ取每一个可能值的概率,使得到所要求的概率分布列.
至于第(Ⅱ)问,可直接应用离散型随机变量数学期望的计算公式求解.
因为ξ是A队赛后所得的总分,根据题意,ξ只可能取0,1,2,3等4个值,其表示的随机事件分别为:
ξ=表示A队3场比赛都输球,全负;
ξ=1表示A队3场比赛中1胜2负;
ξ=2表示A队3场比赛中2胜1负;
ξ=3表示A队3场比赛全胜.
所以由给出的胜负概率表,应用互斥事件概率的加法公式、独立事件的概率加法公式等相关公式,便可求得ξ的分布列.
(Ⅰ)解 ξ、η的可能取值都为3,2,1,0.ξ的分布为:
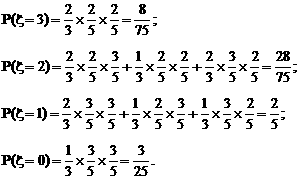
依题意,ξ+η=3,故η的分布为:
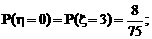
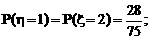
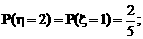
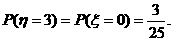
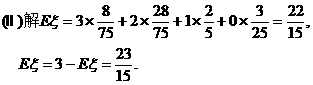
15.某城市在中心广场建造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花.不同的栽种方法有_____种.(以数字作答)
[分析] 本题以花圃设计为应用背景,主要考查排列、组合的基础知识,侧重考查乘法原理和加法原理的应用,以及逻辑思维能力和计数能力.
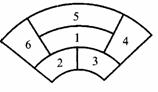
为了正确解答本题,首先必须准确理解题意:抓住花圃布局的要求,看清图形中6个部分的关系;明确每个部分只种同一种颜色的花,相邻部分应种不同颜色的花;而且4种颜色的花都要种上,缺一不可.对这些条件要求,稍有疏忽、遗漏或曲解,都会引致解答出错.其次,应设计好周全而又不出现重复计数的推算程序,关键是推算过程中分步、分类的安排要合理且严密;此外,在每一分步或分类中,计数不出错;最后,乘法原理和加法原理的运用,以及数值计算还得无误,方能得出正确的答数.
采用不同的计数模式和计数程序,伴随出现不同的解法,列举解法供参考.
解法1 将6个区域分4组,不同组栽种不同颜色的花,同一组栽种同一颜色的花.因为区域1与其它5个区域都有公共边,所以为了栽种方案合乎题意,分在同一组的区域至多只能有2个.因而,由图形可知,不同分组法有且只有5类,如下表(表中数字为区域号):
|
|
第一组 |
第二组 |
第三组 |
第四组 |
|
第一类 |
1 |
2 |
3,5 |
4,6 |
|
第二类 |
1 |
2,5 |
3,6 |
4 |
|
第三类 |
1 |
2,5 |
3 |
4,6 |
|
第四类 |
1 |
2,4 |
3,5 |
6 |
|
第五类 |
1 |
2,4 |
3,6 |
5 |
每一类分组法,都有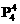 种不同的栽种方法.应用加法原理,得到所有符合题意的不同栽种方法的种数为
种不同的栽种方法.应用加法原理,得到所有符合题意的不同栽种方法的种数为
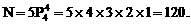
解法2 按区域的顺序,依次安排各区域所栽种的花的颜色:
第1区,可种4色花中的任一种,有4种不同的栽种法;
接着,第2区,因与第1区相邻,两区花色必须不同,所以,第2区只能从3色花中任选一种栽种,有3种不同种法;
跟着,第3区,因与第1、2区都有边界,所以,只有2种不同栽种法;
随后,第4区,与2区无边界,与1、3区都有边界.因此,可分两类情形:
第一类:在第4区中栽种与第2区同一色的花,有1种栽法;至此,只栽种了3种不同颜色的花,因此,第5、6区域,应有一个区域栽种第4种颜色的花,而另一区域可选的花色只有1种(这是因为与之相邻的三个区域,已种上不同颜色的3种花).从而,在第5、6区域栽花的不同方式有2种;
第二类:在第4区域中栽种与第2区域不同颜色的花,有1种栽法;不过,与第一类不同的是:至此,4种不同颜色的花都被栽种了.往后,第5区域栽花有两种选择:一种是栽与第2区域同色花,紧接着,第6区域有2种栽种方法;第五区域另一种栽花法,是栽种与第2区域不同颜色的花,只有1种选择(因为它不能与1、4区域同色),紧接着,由于1、2、5三个区域已栽种3种不同颜色的花,故第6区域只有1种栽花的选择.
综合起来,应用乘法原理和加法原理,得合乎题意的不同栽花的方法种数为
N=4×3×2×(1×2+1×2+1×1)
=120
解法3 因为区域1与其它5个区域都有公共边,所以当区域1栽种一种颜色的花之后,该颜色的花就不能栽于其它区域.因而可分两步走,考虑如下:
第一步,在区域1中,栽上一种颜色的花,有4种栽法;
第二步,在剩下的五个区域中,栽种其它三种颜色的花.为此,可将2至6号五个区域分成3组,使同一组中的不同区域没有公共边.这样的分组法有且只有5类,如下表(表中数字为区域号):
|
|
第一组 |
第二组 |
第三组 |
|
第一类 |
2 |
3,5 |
4,6 |
|
第二类 |
2,4 |
3,5 |
6 |
|
第三类 |
2,4 |
3,6 |
5 |
|
第四类 |
2,5 |
3,6 |
4 |
|
第五类 |
2,5 |
3 |
4,6 |
对每一类分得的3个组,将3种颜色的花分别栽于各组,共有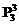 种栽法.
种栽法.
应用乘法原理和加法原理,得合乎题意要求的不同栽种方法的种数为
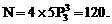
解法4 由于第1、2、3区两两都有边界,所以这3个区所栽的花,彼此必须不同颜色.因而,第一步可从4种颜色的花任取3种分别栽在这3个区域上,共有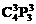 种栽法.其次将另一颜色的花栽于4、5、6三个区中的一个区或两个区,即分为两类情形:
种栽法.其次将另一颜色的花栽于4、5、6三个区中的一个区或两个区,即分为两类情形:
第一类:栽在4、5、6的一个区域中,有3种情形:
情形1:栽于4区,则6区只有一种颜色的花可栽(因为必须不同于4、1、2区的颜色),进而,5区周边三个区域已栽上3种不同颜色的花,故5区也只有一种颜色的花可栽;
情形2:栽于6区,则与情形1同理,4、5区域分别只有1种颜色可栽;
情形3:栽于5区,由于5、1、2三个区已栽上不同颜色的花,6区只有1种栽法;同理,4区也只有1种栽法.
第二类:栽于4、5、6中的两个区,只有栽于4、6两个区域的一种情形,这时5区有2种栽法(因为5区的周边只有两色花).
综合起来,应用乘法原理与加法原理,得不同栽种方法的种数为
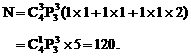
解法5 分两类情况考虑:
第1类:第1、2、3、5等四个区域栽种不同颜色的4种花,共有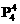 种栽法.对于每一种栽法,第4、6区分别都只有1种颜色的花可栽.
种栽法.对于每一种栽法,第4、6区分别都只有1种颜色的花可栽.
第2类:第1、2、3、5等四个区域栽种不同颜色的3种花,共有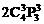 种栽法.对于每一种栽法,要么2、5区栽同色花,要么3、5区栽同色花.对于前者,第6区有2种颜色的花可供选栽,第4区只能栽第4种颜色的花;对于后者,第4区有2种颜色的花可供选栽,第6区只能栽第4种颜色的花.即无论何种情形,第4、6区的栽法都是2种.
种栽法.对于每一种栽法,要么2、5区栽同色花,要么3、5区栽同色花.对于前者,第6区有2种颜色的花可供选栽,第4区只能栽第4种颜色的花;对于后者,第4区有2种颜色的花可供选栽,第6区只能栽第4种颜色的花.即无论何种情形,第4、6区的栽法都是2种.
综合上述情形,应用加法原理与乘法原理,得不同栽种方法的种数为
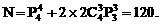
[答案] 120
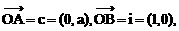 直线
直线 分别过点O和A,其方向向量分别为c+λi和i-2λc,点P是
分别过点O和A,其方向向量分别为c+λi和i-2λc,点P是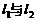 的交点.为了求点P的轨迹方程,可采用不同的方法.在这里,有一点值得注意的是:试题本身并没有要求考生求点P的轨迹方程,我们是借助轨迹的思想,只须求出点P的坐标所应满足的方程,进而展开讨论,而无须检验满足方程的每一个解为坐标的点都是符合题意的点P,也即无须要求所得方程的纯粹性,与严格意义上的求轨迹方程有所不同.
的交点.为了求点P的轨迹方程,可采用不同的方法.在这里,有一点值得注意的是:试题本身并没有要求考生求点P的轨迹方程,我们是借助轨迹的思想,只须求出点P的坐标所应满足的方程,进而展开讨论,而无须检验满足方程的每一个解为坐标的点都是符合题意的点P,也即无须要求所得方程的纯粹性,与严格意义上的求轨迹方程有所不同.

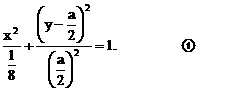
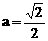 时,方程①是圆方程,故不存在合乎题意的定点E和F;
时,方程①是圆方程,故不存在合乎题意的定点E和F;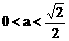 时,方程①表示椭圆,故焦点
时,方程①表示椭圆,故焦点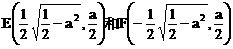 为合乎题意的两个定点;
为合乎题意的两个定点;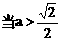 时,方程①也表示椭圆,故焦点
时,方程①也表示椭圆,故焦点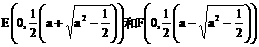 为合乎题意的两个定点.
为合乎题意的两个定点.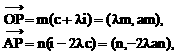
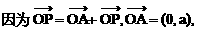
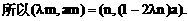
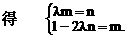
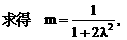
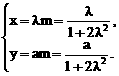
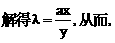
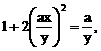
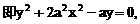
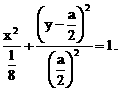
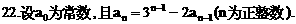
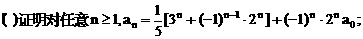
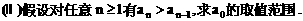
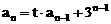 ”.理科试题改变以往给出初始值的做法,给出常数
”.理科试题改变以往给出初始值的做法,给出常数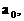 证明数列
证明数列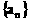 的一个通项公式。这种提问方式反映出新的考查角度,不让考生死套题型,有利于考查独立思考能力和理性思维能力,对文科考生则降低抽象思维的要求,递推关系简化为基本形式“
的一个通项公式。这种提问方式反映出新的考查角度,不让考生死套题型,有利于考查独立思考能力和理性思维能力,对文科考生则降低抽象思维的要求,递推关系简化为基本形式“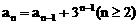 ”,并给出初始值a=1,使试题难度较为切合文科考生的实际.
”,并给出初始值a=1,使试题难度较为切合文科考生的实际.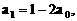 等式成立;
等式成立;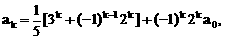
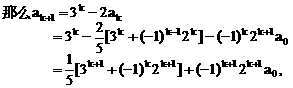
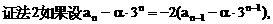
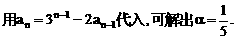
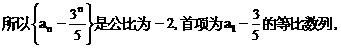
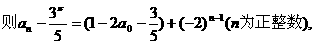
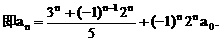
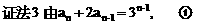
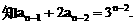
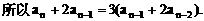
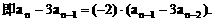

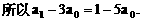
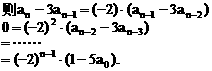
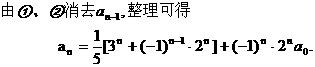
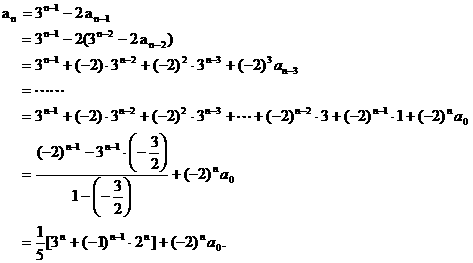
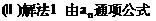
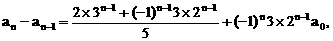
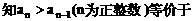
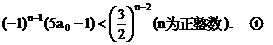
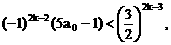
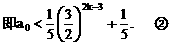
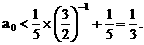
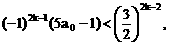
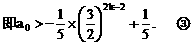
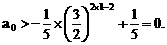
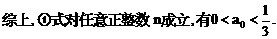

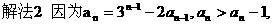
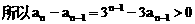
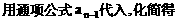
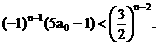
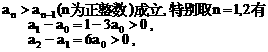
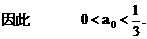
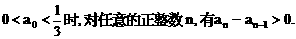
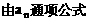
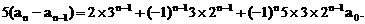
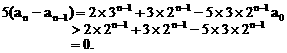
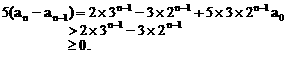

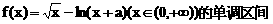 .
.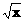 与对数函数ln(x+a)之差,让考生求这个函数的单调区间.直接应用单调函数的定义,难以进行有效的讨论,宜借助求导的方法求解.以此可以考查函数求导的技能,以及讨论导数正负性的方法.
与对数函数ln(x+a)之差,让考生求这个函数的单调区间.直接应用单调函数的定义,难以进行有效的讨论,宜借助求导的方法求解.以此可以考查函数求导的技能,以及讨论导数正负性的方法.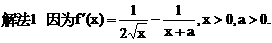
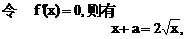
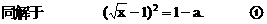
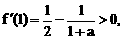
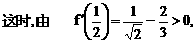
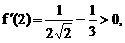
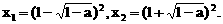
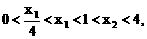
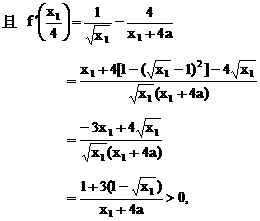
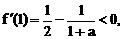
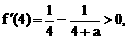
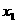 或
或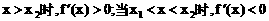
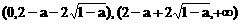 都是单调区间,f(x)在这两个区间上都是增函数;
都是单调区间,f(x)在这两个区间上都是增函数;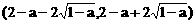 也是单调区间,f(x)在这个区间上是减函数.
也是单调区间,f(x)在这个区间上是减函数.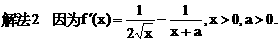
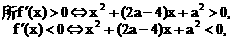
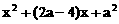
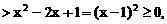
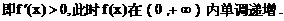
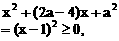
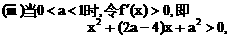
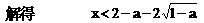
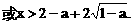
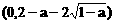 内单调递增,在区间
内单调递增,在区间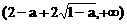 内也单调递增.
内也单调递增.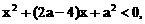
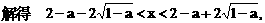
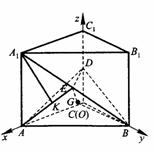
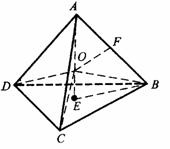
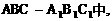 底面是等腰直角三角形,∠ACB=90°.侧棱
底面是等腰直角三角形,∠ACB=90°.侧棱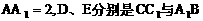 的中点,点E在平面ABD上的射影是△ABD的重心G.
的中点,点E在平面ABD上的射影是△ABD的重心G.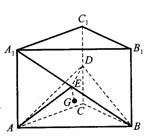
 与平面ABD所成角的大小(结果用反三角函数值表示);
与平面ABD所成角的大小(结果用反三角函数值表示);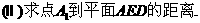
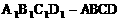 的棱
的棱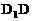 的中点,则正方体的中心O在截面AMC上的射影恰好是△AMC的重心”.试题基本上是采用其逆命题,且只给出半个正方体,把问题提为“正方体的一条对角线与截面所成的角”,隐蔽了上述性质,提高了对考生空间想像力和推理能力的要求,以期更好地考查考生的数学能力.
的中点,则正方体的中心O在截面AMC上的射影恰好是△AMC的重心”.试题基本上是采用其逆命题,且只给出半个正方体,把问题提为“正方体的一条对角线与截面所成的角”,隐蔽了上述性质,提高了对考生空间想像力和推理能力的要求,以期更好地考查考生的数学能力.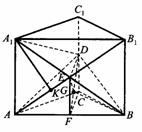
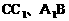 的中点,又DC⊥平面ABC,
的中点,又DC⊥平面ABC,
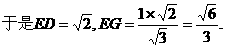
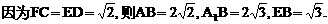
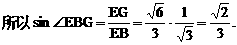

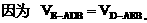
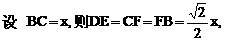
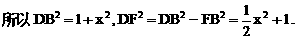
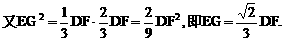
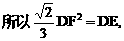
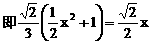
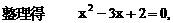

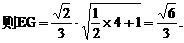
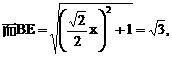
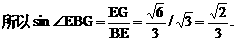

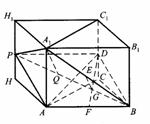
 的中点P,连结PD,PA,PB,则ABDP是平行四边形,PB必过△ADB的重心.
的中点P,连结PD,PA,PB,则ABDP是平行四边形,PB必过△ADB的重心.
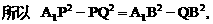
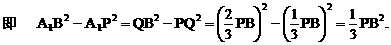
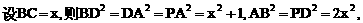
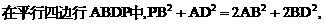
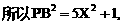


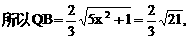
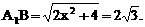
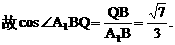

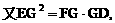
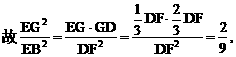
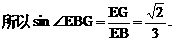
 与平面ABD所成的角.
与平面ABD所成的角.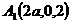 ,E(a,a,1),
,E(a,a,1),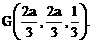
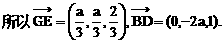
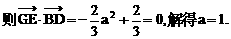
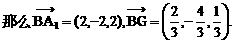
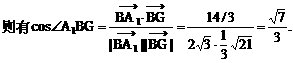
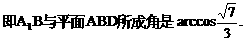


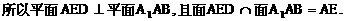
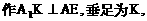
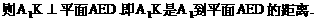
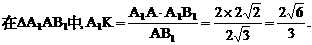
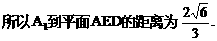

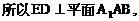
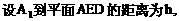
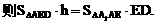
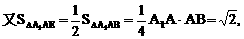
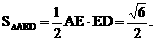
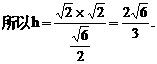

 E(1,1,1),D(0,0,1).
E(1,1,1),D(0,0,1).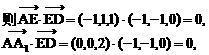
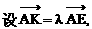
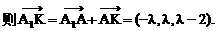
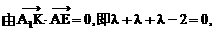
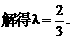
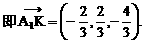
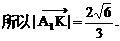

 上的图象.
上的图象.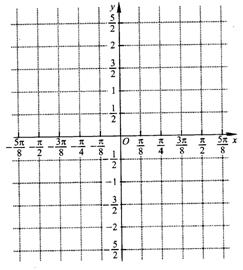

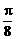
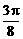
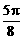
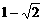
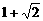
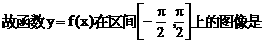
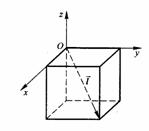
 ⊥面MNP的图形的序号是_______.(写出所有符合要求的图形序号)
⊥面MNP的图形的序号是_______.(写出所有符合要求的图形序号)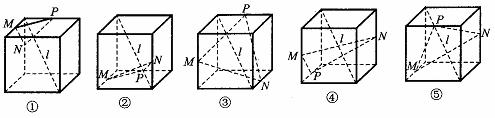
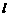 位置固定,截面MNP变动,
位置固定,截面MNP变动, 如附图,与题设图形对比讨论.在附图中,三个截面
如附图,与题设图形对比讨论.在附图中,三个截面 都是对角线
都是对角线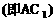 的垂面.
的垂面.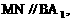 MP∥BD,
MP∥BD,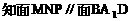 ,故得
,故得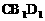 相交,而过交点且与
相交,而过交点且与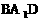 相交,知
相交,知 故
故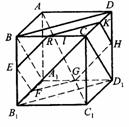
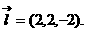
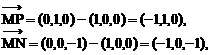
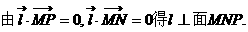
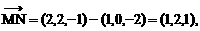

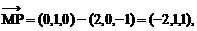


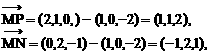
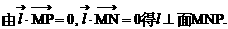
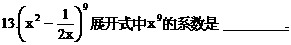
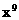 的系数,如解法1.由于二项式中的两个项都含有x,因此将其适当变形,有利于简化计算,如解法2.试题的这种设计,体现了对计算灵活性和准确性的要求.
的系数,如解法1.由于二项式中的两个项都含有x,因此将其适当变形,有利于简化计算,如解法2.试题的这种设计,体现了对计算灵活性和准确性的要求.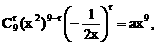
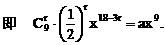
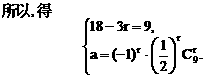
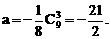
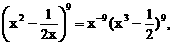

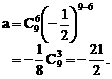
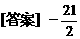
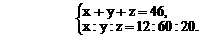
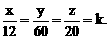
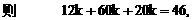
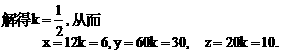

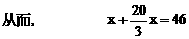

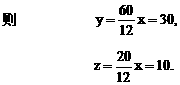
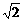 ,四个顶点在同一球面上,则此球的表面积为
,四个顶点在同一球面上,则此球的表面积为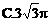 D.6π
D.6π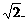 .
.
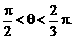
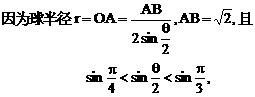
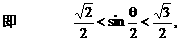
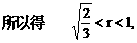

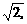 得
得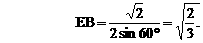
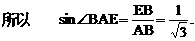
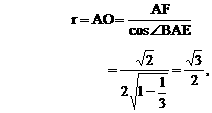

 则四面体
则四面体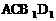 的棱长都为
的棱长都为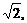 它的外接球也是正方体的外接球,其半径为正方体对角线长
它的外接球也是正方体的外接球,其半径为正方体对角线长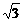 的一半,即有
的一半,即有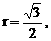 故所求球面积为S=3π.
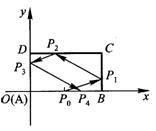
故所求球面积为S=3π.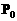 沿与AB夹角为θ的方向射到BC上的点
沿与AB夹角为θ的方向射到BC上的点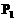 后,依次反射到CD、DA和AB上的点
后,依次反射到CD、DA和AB上的点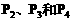 (入射角等于反射角).设
(入射角等于反射角).设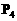 的坐标为
的坐标为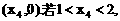 则tanθ的取值范围是
则tanθ的取值范围是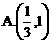
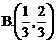
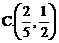
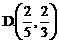
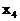 是tanθ的函数,试题要求由
是tanθ的函数,试题要求由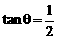 时,根据反射原理,得点
时,根据反射原理,得点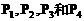 依次是BC,CD,DA和AB的中点,即有
依次是BC,CD,DA和AB的中点,即有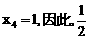 不属于所求的tanθ的取值范围.从而,可排除选项A、B和D,应取C作答.
不属于所求的tanθ的取值范围.从而,可排除选项A、B和D,应取C作答.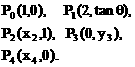

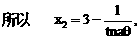
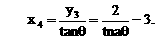
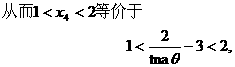

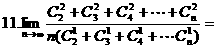
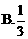
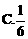 D.6
D.6