(1)已知集合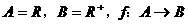 是从集合A到B的一个映射,若
是从集合A到B的一个映射,若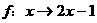 ,则B中的元素3的原象为
,则B中的元素3的原象为
(A)-1 (B)1 (C)2 (D)3
(2)已知命题甲为x>0;命题乙为|x|>0,那么
(A)甲是乙的充分非必要条件
(B)甲是乙的必要非充分条件
(C)甲是乙的充要条件
(D)甲既不是乙的充分条件,也不是乙的必要条件
(3)下列函数中,周期为π的奇函数是
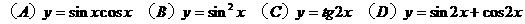
(4)在复平面中,已知点A(2,1),B(0,2),C(-2,1),O(0,0)。给出下面的结论:
①直线OC与直线BA平行; ②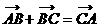 ;
;
③ ;
④
;
④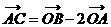 。
。
其中正确结论的个数是
(A)1个 (B)2个 (C)3个 (D)4个
(5)过原点的直线与圆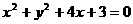 相切,若切点在第二象限,则该直线的方程是
相切,若切点在第二象限,则该直线的方程是 
(6)在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1:3,则锥体被截面所分成的两部分的体积之比为
(A) (B)1:9 (C)
(B)1:9 (C)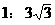 (D)
(D)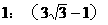
(7)将4张互不相同的彩色照片与3张互不相同的黑白照片排成一排,任何两张黑白照片都不相邻的不同排法的种数是
(A)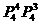 (B)
(B)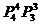 (C)
(C)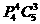 (D)
(D)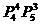
(8)已知数列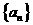 的通项公式是
的通项公式是 ,其中a,b均为正常数,那么
,其中a,b均为正常数,那么
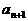 的大小关系是
的大小关系是
(A)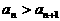 (B)
(B)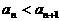 (C)
(C)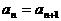 (D)与n的取值相关
(D)与n的取值相关
(9)双曲线的虚轴长为4,离心率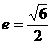 ,
,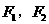 分别是它的左、右焦点,若过
分别是它的左、右焦点,若过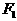 的直线与双曲线的左支交于A,B两点,且|AB|是
的直线与双曲线的左支交于A,B两点,且|AB|是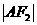 与
与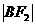 的等差中项,则|AB|等于
的等差中项,则|AB|等于
(A) (B)
(B)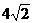 (C)
(C)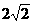 (D)8
(D)8
(10)某农贸市场出售西红柿,当价格上涨时,供给量相应增加,而需求量相应减少,具体调查结果如下表:
表1 市场供给表
|
单价(元/kg) |
2 |
2.
4 |
2.
8 |
3.
2 |
3.
6 |
4 |
|
供给量(1000kg) |
50 |
60 |
70 |
75 |
80 |
90 |
表2 市场需求表
|
单价(元/kg) |
4 |
3.
4 |
2.
9 |
2.
6 |
2.
3 |
2 |
|
需求量(1000kg) |
50 |
60 |
65 |
70 |
75 |
80 |
根据以上提供的信息,市场供需平衡点(即供给量和需求量相等时的单价)应在区间
(A)(2. 3,2. 6)内 (B)(2. 4,2. 6)内
(C)(2. 6,2. 8)内 (D)(2. 8,2. 9)内
第Ⅱ卷(非选择题共100分)

 在定义域上是( )
在定义域上是( ) (B)
(B)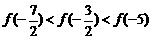
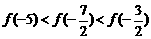 (D)
(D)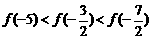
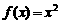 ,集合
,集合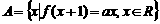 ,且
,且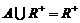 ,则实数a的取值范围是( )
,则实数a的取值范围是( )
 的图像关于y=x对称,则f(2x-x2)的单调递增区间是( )
的图像关于y=x对称,则f(2x-x2)的单调递增区间是( )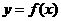 是R上的增函数,则
是R上的增函数,则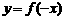 在R上( )
在R上( )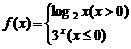 则
则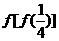 的值为( )
的值为( ) (C)-9 (D)
(C)-9 (D)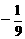
 ,求tg2x的值。
,求tg2x的值。 中,E、F分别为
中,E、F分别为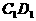 与AB的中点。
与AB的中点。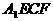 是菱形;
是菱形;
 一平面
一平面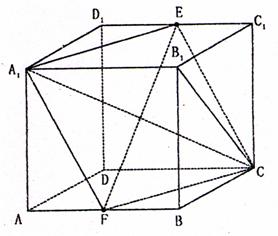
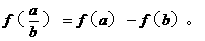
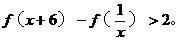 。
。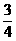 的直线交双曲线的两条准线于M,N两点,以MN为直径的圆过原点,求此双曲线的方程。
的直线交双曲线的两条准线于M,N两点,以MN为直径的圆过原点,求此双曲线的方程。 。
。 ,其中p > 0,p + q > 1。对于数列
,其中p > 0,p + q > 1。对于数列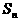 ,且
,且 (n∈N)。
(n∈N)。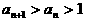 ;
;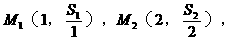
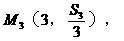 …,
…,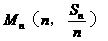 都在同一直线上。
都在同一直线上。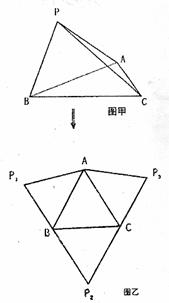
 的值为______。
的值为______。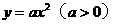 上一点A到此抛物线的焦点的距离为
上一点A到此抛物线的焦点的距离为 ,那么点A的坐标为_______。
,那么点A的坐标为_______。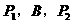 共线,
共线,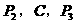 共线,且
共线,且 ,则在三棱锥P-ABC中,PA与BC所成的角的大小是___________。
,则在三棱锥P-ABC中,PA与BC所成的角的大小是___________。