0 446344 446352 446358 446362 446368 446370 446374 446380 446382 446388 446394 446398 446400 446404 446410 446412 446418 446422 446424 446428 446430 446434 446436 446438 446439 446440 446442 446443 446444 446446 446448 446452 446454 446458 446460 446464 446470 446472 446478 446482 446484 446488 446494 446500 446502 446508 446512 446514 446520 446524 446530 446538 447348
 (13)用平面
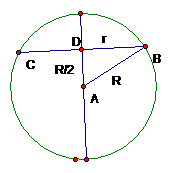
(13)用平面 截半径为R的球,如果球心到平面
截半径为R的球,如果球心到平面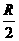 ,那么截得小圆的面积与球的表面积的比值为______________.
,那么截得小圆的面积与球的表面积的比值为______________. ,球的半径是R, 画一个轴截面图形. 在
,球的半径是R, 画一个轴截面图形. 在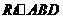 中,显然,
中,显然,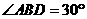 ,于是
,于是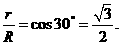
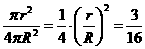 ,应填
,应填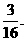
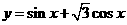 在区间
在区间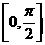 上的最小值为_____________.
上的最小值为_____________.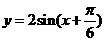 . 由
. 由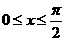 ,得
,得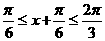 . 于是,函数的最小值为
. 于是,函数的最小值为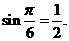 应填
应填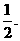
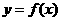 是奇函数,当
是奇函数,当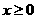 时,
时,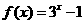 . 设
. 设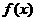 的反函数是
的反函数是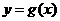 ,则
,则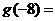 ________.
________.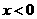 时,
时, . 这样由
. 这样由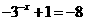 ,解得
,解得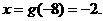 应填
应填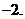
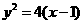 上的一个动点,则点P到点
上的一个动点,则点P到点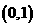 的距离与点P到
的距离与点P到 轴的距离之和的最小值是______________.
轴的距离之和的最小值是______________.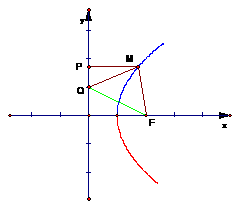 讲解:显然,
讲解:显然,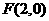 是抛物线的焦点,于是
是抛物线的焦点,于是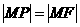 .
. 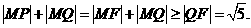
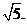
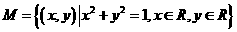 ,
,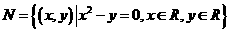 ,则集合
,则集合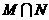 中元素的个数为( )
中元素的个数为( )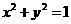 和抛物线
和抛物线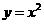 的图形,易知它们有两个交点,应选B.
的图形,易知它们有两个交点,应选B.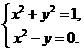
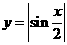 的最小正周期是( )
的最小正周期是( )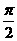 B.
B. 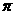 C.
C.
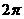 D.
D.
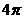
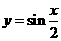 的一半.
的一半.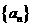 是等差数列,且
是等差数列,且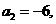
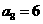 ,
,  是数列
是数列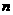 项的和,则( )
项的和,则( )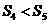 B.
B.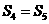 C.
C.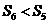 D.
D.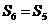
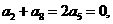 即
即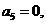 于是
于是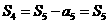 ,应选B.
,应选B.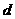 ,则有已知,得
,则有已知,得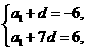 解出
解出 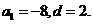 于是
于是 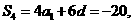
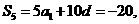
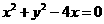 在点
在点 处的切线方程是( )
处的切线方程是( )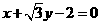 B.
B.
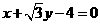
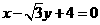 D.
D.
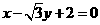
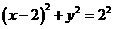 ,圆心
,圆心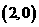 到直线
到直线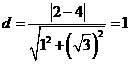 ,不是圆的半径2,故应选D.
,不是圆的半径2,故应选D.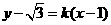 ,即
,即 ,
, 解出
解出 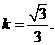
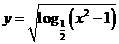 的定义域是( )
的定义域是( )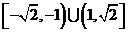 B.
B.
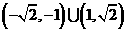

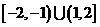 D.
D.
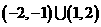
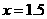 ,有
,有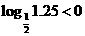 ,否定C, D; 取
,否定C, D; 取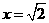 ,有
,有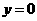 ,否定B. 应选A.
,否定B. 应选A.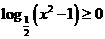 ,即
,即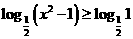 , 等价于
, 等价于 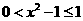 .
.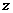 的幅角的主值为
的幅角的主值为 ,虚部为
,虚部为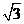 ,则
,则 ( )
( )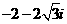 B.
B.
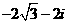
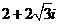 D.
D.
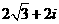
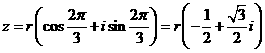 , 则有
, 则有 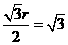 ,
,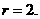 于是
于是 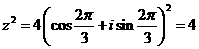
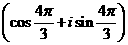 =
=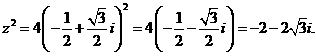
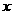 轴上,两条渐近线为
轴上,两条渐近线为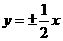 ,则双曲线的离心率
,则双曲线的离心率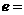 ( )
( )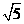 C.
C. 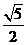 D.
D.
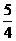
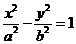 ,其两条渐近线为
,其两条渐近线为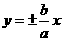 ,于是
,于是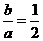 ,即有
,即有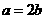 ,有
,有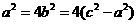 ,
,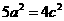 ,即
,即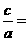
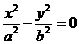 ,也就是
,也就是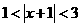 的解集为( )
的解集为( )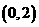 B.
B.
 C.
C. 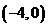 D.
D. 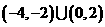
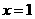 ,适合不等式,否定C; 取
,适合不等式,否定C; 取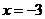 ,适合不等式,否定A, B. 应选D.
,适合不等式,否定A, B. 应选D.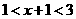 或
或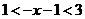 ,即
,即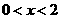 或
或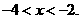
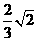 B.
B. 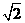 C.
C. 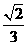 D.
D. 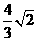
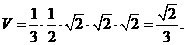 应选C.
应选C. 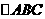 中,
中,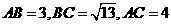 ,则边
,则边 上的高为( )
上的高为( )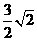 B.
B.
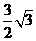 C.
C.
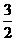 D.
D.
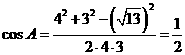 ,得
,得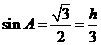 ,有
,有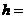
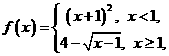 则使得
则使得 的自变量
的自变量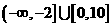 B.
B. 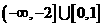
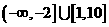 D.
D.
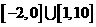
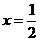 ,有
,有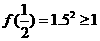 成立,否定C, D;取
成立,否定C, D;取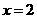 ,
,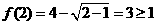 成立,否定B. 应选A.
成立,否定B. 应选A. 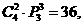 应选C.
应选C.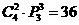 的实际意义. 再想想:解法
的实际意义. 再想想:解法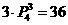 是否正确?
是否正确?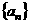 的前
的前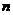 项和
项和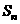 满足
满足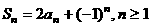
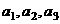 ;
;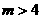 ,有
,有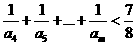 .
.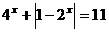
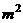 的矩形蔬菜温室。在温室内,沿左、右两端与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左、右两端与后侧内墙各保留1 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3




 设AB=BC=
设AB=BC=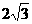 ,求AC与平面PBC所成角的大小.
,求AC与平面PBC所成角的大小.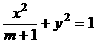 的两个焦点是
的两个焦点是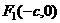 与
与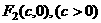 ,且椭圆上存在一点
,且椭圆上存在一点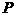 ,使得直线
,使得直线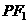 与
与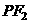 垂直.
垂直.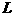 是相应于焦点
是相应于焦点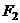 的准线,直线
的准线,直线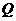 ,若
,若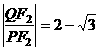 ,求直线
,求直线 为锐角,且
为锐角,且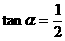 ,求
,求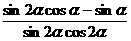 的值。
的值。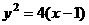 上的一个动点,则点
上的一个动点,则点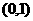 的距离与点
的距离与点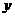 轴的距离之和的最小值为
.
轴的距离之和的最小值为
.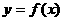 是奇函数,当
是奇函数,当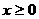 时,
时,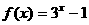 ,设
,设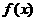 的反函数是
的反函数是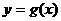 ,则
,则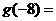 .
.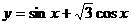 在区间
在区间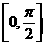 上的最小值为
.
上的最小值为
. 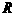 的球,如果球心到平面
的球,如果球心到平面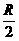 ,那么截得小圆的面积与球的表面积的比值为
.
,那么截得小圆的面积与球的表面积的比值为
.