0 446338 446346 446352 446356 446362 446364 446368 446374 446376 446382 446388 446392 446394 446398 446404 446406 446412 446416 446418 446422 446424 446428 446430 446432 446433 446434 446436 446437 446438 446440 446442 446446 446448 446452 446454 446458 446464 446466 446472 446476 446478 446482 446488 446494 446496 446502 446506 446508 446514 446518 446524 446532 447348
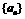 中,
中,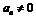 ,若
,若 ,且
,且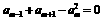 ,
, ,则
,则 等于
等于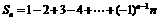 ,则
,则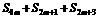 (
( N*)的值为
N*)的值为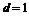 ,
,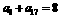 ,则
,则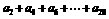 的值为
的值为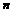 项和
项和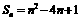 ,则
,则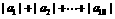 的值为
的值为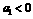 ,则
,则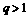 (B)
(B)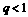 (C)
(C)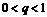 (D)
(D)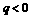
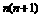 }中的一项
}中的一项
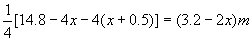 。
由3.2-2x>0且x>0,得0<x<1.6。
设容器的容积为ym3,则有y=x(x+0.5)(3.2-2x)=-2x3+2.2x2+1.6x,
(0<x<1.6)
∴ y'=-6x2+4.4x+1.6=0,
即15x2-11x-4=0,解得
。
由3.2-2x>0且x>0,得0<x<1.6。
设容器的容积为ym3,则有y=x(x+0.5)(3.2-2x)=-2x3+2.2x2+1.6x,
(0<x<1.6)
∴ y'=-6x2+4.4x+1.6=0,
即15x2-11x-4=0,解得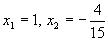 (不合题意,舍去)。
当x∈(0,1)时,y'>0;当x∈(1,1.6)时,y'<0。
∴ 函数y=-2x3+2.2x2+1.6x在(0,1)上单调递增,在[1,1.6]上单调递减。
因此,当x=1时,ymax=-2+2.2+1.6=1.8,这时,高为3.2-2×1=1.2。
故容器的高为1.2m时容器最大,最大容积为1.8m3。
例11.一艘渔艇停泊在距岸9km处,今需派人送信给距渔艇
(不合题意,舍去)。
当x∈(0,1)时,y'>0;当x∈(1,1.6)时,y'<0。
∴ 函数y=-2x3+2.2x2+1.6x在(0,1)上单调递增,在[1,1.6]上单调递减。
因此,当x=1时,ymax=-2+2.2+1.6=1.8,这时,高为3.2-2×1=1.2。
故容器的高为1.2m时容器最大,最大容积为1.8m3。
例11.一艘渔艇停泊在距岸9km处,今需派人送信给距渔艇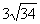 km处的海岸渔站,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸再步行可以使抵达渔站的时间最省?
解析:如图示设A点为渔艇处,BC为海岸线,C为渔站,且AB=9km,
设D为海岸线上
km处的海岸渔站,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸再步行可以使抵达渔站的时间最省?
解析:如图示设A点为渔艇处,BC为海岸线,C为渔站,且AB=9km,
设D为海岸线上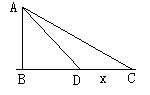 一点,CD=x,只需将时间T表示为x的函数,
∵
一点,CD=x,只需将时间T表示为x的函数,
∵ 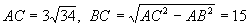 ,
由A到C的时间T,则
,
由A到C的时间T,则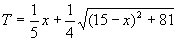 (0≤x≤15)
(0≤x≤15)
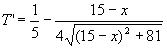 (0≤x≤15)
令T'=0,解得x=3,在x=3附近,T'由负到正,
因此在x=3处取得最小值,又
(0≤x≤15)
令T'=0,解得x=3,在x=3附近,T'由负到正,
因此在x=3处取得最小值,又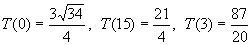 ,比较可知T(3)最小。
训练题:
1.函数y=4x2(x-2), x∈[-2,2]的最小值是_____。
2.一个外直径为10cm的球,球壳厚度为
,比较可知T(3)最小。
训练题:
1.函数y=4x2(x-2), x∈[-2,2]的最小值是_____。
2.一个外直径为10cm的球,球壳厚度为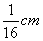 ,则球壳体积的近似值为____。
3.函数f(x)=x4-5x2+4的极大值是______,极小值是_____。
4.做一个容积为256升的方底无盖水箱,问高为多少时最省材料?
参考答案:
1. –64 2. 19.63cm3 3. 4;
,则球壳体积的近似值为____。
3.函数f(x)=x4-5x2+4的极大值是______,极小值是_____。
4.做一个容积为256升的方底无盖水箱,问高为多少时最省材料?
参考答案:
1. –64 2. 19.63cm3 3. 4;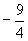 4. 设高为h,底边长为a,则所用材料为S=a2+4ah,而a2h=256,a∈(0,+∞),
∴
4. 设高为h,底边长为a,则所用材料为S=a2+4ah,而a2h=256,a∈(0,+∞),
∴ 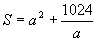 , a∈(0,+∞), 令S'(a)=
, a∈(0,+∞), 令S'(a)=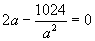 ,
∴ a=8。
显然当0<a<8时,S'(a)<0,当a>8时,S'(a)>0,因此当a=8时,S最小,此时h=4。
,
∴ a=8。
显然当0<a<8时,S'(a)<0,当a>8时,S'(a)>0,因此当a=8时,S最小,此时h=4。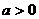 ,求函数
,求函数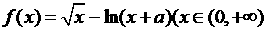 的单调区间.
的单调区间.