0 446386 446394 446400 446404 446410 446412 446416 446422 446424 446430 446436 446440 446442 446446 446452 446454 446460 446464 446466 446470 446472 446476 446478 446480 446481 446482 446484 446485 446486 446488 446490 446494 446496 446500 446502 446506 446512 446514 446520 446524 446526 446530 446536 446542 446544 446550 446554 446556 446562 446566 446572 446580 447348
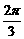 弧长到达Q点,则Q的坐标为
(A)(-
弧长到达Q点,则Q的坐标为
(A)(- ,
,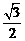 ) (B) (-
) (B) (-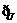 (M
(M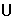 N)=
(A){1,2,3} (B){2} (C){1,3,4} (D){4}
N)=
(A){1,2,3} (B){2} (C){1,3,4} (D){4}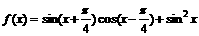 ,求
,求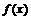 的最大值及取最大时
的最大值及取最大时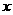 的集合.
的集合. (18)(本小题满分12分)如图,四面体
(18)(本小题满分12分)如图,四面体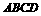 中,
中, 与
与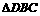 都是边长为4的正三角形
都是边长为4的正三角形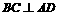
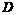 到平面
到平面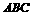 的距离不小于3,求二面角
的距离不小于3,求二面角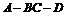 的平面角的取值范围
的平面角的取值范围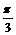 时,求点
时,求点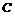 到平面
到平面 的距离.
的距离.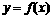 定义域为
定义域为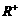 ,且对任意的
,且对任意的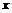 、
、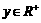 ,恒有
,恒有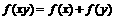 ,
,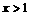 时,
时,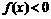
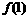 的值,并证明
的值,并证明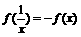
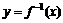 的定义域内恒有
的定义域内恒有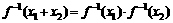
 到定点
到定点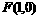 的距离比它到定直线
的距离比它到定直线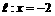 的距离小1
的距离小1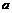 ,使得在直线
,使得在直线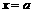 上存在唯一点
上存在唯一点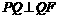 ,若存在,求出常数
,若存在,求出常数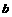 元,填海湾造地后的每亩土地的年平均收益为
元,填海湾造地后的每亩土地的年平均收益为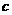 元(其中
元(其中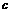 均为常数)
均为常数)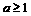 时,函数
时,函数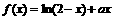 在开区间
在开区间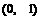 内是增函数;当
内是增函数;当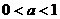 时,函数
时,函数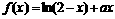 在开区间
在开区间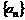 满足
满足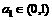 ,
,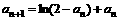 (
(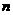 为正整数),
为正整数),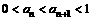
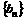 满足
满足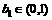 ,
,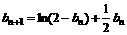 (
(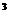 的近似值(精确到0.001)为__________________.
的近似值(精确到0.001)为__________________. 中,
中,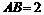 ,线段
,线段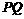 在
在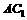 上运动,且
上运动,且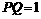 ,则四面体
,则四面体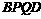 的体积为_____________________.
的体积为_____________________.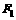 、
、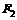 ,椭圆上满足
,椭圆上满足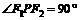 的点
的点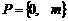
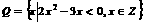 ,若
,若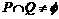 ,则
,则 的值为
的值为 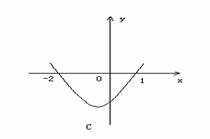 (2)不等式
(2)不等式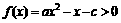 的解集为
的解集为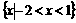 ,则函数
,则函数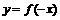 的图象为
的图象为 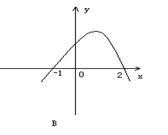
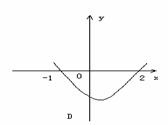
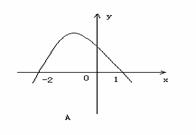
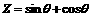 且
且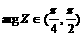 ,则
,则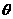 的一个取值区间为
的一个取值区间为
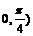 (B)
(B)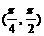 (C)
(C)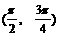 (D)
(D)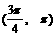
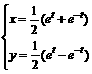 (
(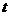 为参数)化为普通方程是
为参数)化为普通方程是
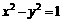 (B)
(B)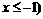 (C)
(C)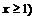 (D)
(D)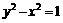
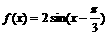 ,给出下列命题,其中正确的是
,给出下列命题,其中正确的是
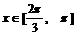 时,
时,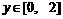
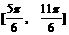 上是增函数
上是增函数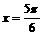 对称
对称 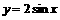 的图象向左平移
的图象向左平移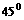 处,当行驶1小时后,汽车在北偏东
处,当行驶1小时后,汽车在北偏东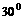 处,则汽车行驶的速度为
处,则汽车行驶的速度为
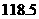 (C)118
(D)117
(C)118
(D)117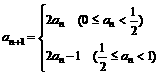 若
若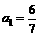 ,则
,则
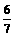 (B)
(B)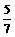 (C)
(C)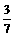 (D)
(D)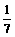
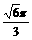 (B)
(B)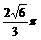 (C)
(C)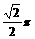 (D)
(D)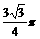
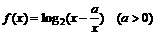 在区间
在区间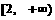 上是增函数,则
上是增函数,则 (B)
(B)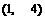 (C)
(C)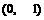 (D)
(D)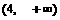
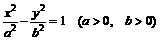 与抛物线
与抛物线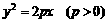 交于
交于 、
、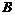 两点,若直线
两点,若直线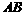 既过双曲线的焦点,又过抛物线的焦点,则此双曲线的离心率为
既过双曲线的焦点,又过抛物线的焦点,则此双曲线的离心率为 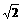 (B)
(B)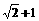 (C)2
(D)3
(C)2
(D)3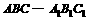 中,
中,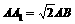 ,则异面直线
,则异面直线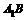 与
与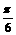 B.
B. C.
C.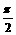
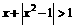
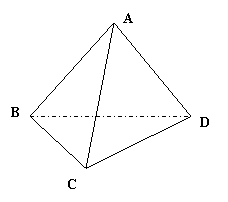 (18)(本小题满分12分)如图,四面体
(18)(本小题满分12分)如图,四面体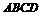 中,
中,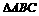 与
与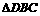 都是边长为4的正三角形
都是边长为4的正三角形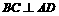
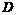 到平面
到平面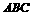 的距离不小于3,求二面角
的距离不小于3,求二面角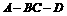 的平面角的取值范围
的平面角的取值范围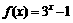 的反函数
的反函数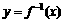 ,
,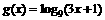
 ,求
,求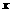 的取值范围
的取值范围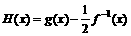 ,当
,当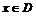 时,求
时,求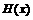 的值域
的值域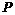 到定点
到定点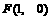 的距离比它到定直线
的距离比它到定直线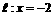 的距离小1
的距离小1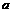 ,使得在直线
,使得在直线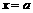 上存在唯一点
上存在唯一点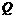 ,满足
,满足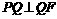 ,若存在,求出常数
,若存在,求出常数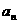 }的前
}的前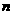 项和为
项和为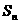 ,
,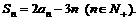
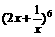 的展开式中的常数项为__________________.
的展开式中的常数项为__________________.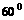 二面角,坡脚的水平线
二面角,坡脚的水平线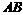 上有两点
上有两点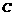 ,乙沿水平面自
,乙沿水平面自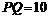 米,则此时甲、乙两人间的直线距离为约_______________(精确到
米,则此时甲、乙两人间的直线距离为约_______________(精确到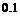 米).
米).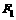 、
、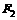 ,椭圆上满足
,椭圆上满足 的点
的点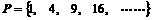 ,若
,若 ,
,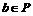 ,则
,则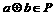 ,则运算
,则运算 可能是
可能是 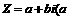 、
、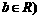 ,则
,则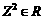 的充要条件是
的充要条件是
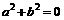 (B)
(B) (C)
(C)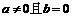 (D)
(D)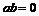
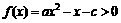 的解集为
的解集为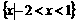 ,则函数
,则函数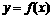 的图象为
的图象为 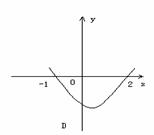
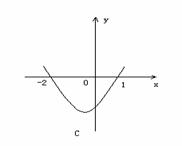
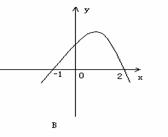
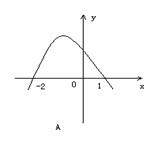
 ,则
,则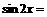
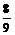 (B)
(B)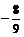 (C)
(C)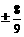 (D)
(D)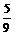
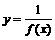 是
是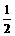 (B)偶函数,最大值为
(B)偶函数,最大值为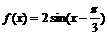 ,给出下列命题,其中正确的是
,给出下列命题,其中正确的是
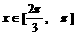 时,
时,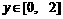
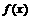 在区间
在区间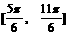 上是增函数
上是增函数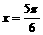 对称
对称 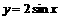 的图象向左平移
的图象向左平移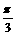 个单位得到
个单位得到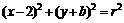 与直线
与直线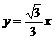 和
和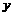 轴都相切,则
轴都相切,则 =
=
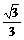 (D)与
(D)与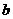 有关
有关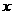 、
、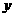 之间插入数
之间插入数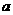 ,使之成为等差数列,又
,使之成为等差数列,又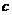 使之成为等比数列,则有
使之成为等比数列,则有
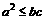 (C)
(C)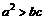 (C)
(C)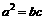 (D)
(D)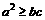
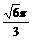 (B)
(B)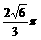 (C)
(C)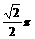 (D)
(D)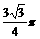
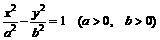 与抛物线
与抛物线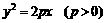 交于
交于 、
、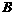 两点,若直线
两点,若直线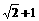 (B)
(B)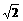 (C)2
(D)3
(C)2
(D)3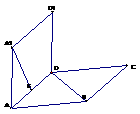 (11)在直二面角
(11)在直二面角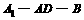 中,四边形
中,四边形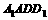 、
、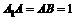 ,
,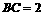 ,
,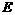 为
为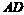 的中点,则异面直线
的中点,则异面直线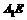 与
与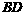 所成角的余弦值为
所成角的余弦值为 (B)
(B)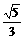 (C)
(C)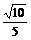 (D)
(D)