0 446404 446412 446418 446422 446428 446430 446434 446440 446442 446448 446454 446458 446460 446464 446470 446472 446478 446482 446484 446488 446490 446494 446496 446498 446499 446500 446502 446503 446504 446506 446508 446512 446514 446518 446520 446524 446530 446532 446538 446542 446544 446548 446554 446560 446562 446568 446572 446574 446580 446584 446590 446598 447348
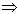 q,则p是q的充分条件
q,则p是q的充分条件 q,则p是q的充要条件,q也是p的充要条件
q,则p是q的充要条件,q也是p的充要条件