0 446384 446392 446398 446402 446408 446410 446414 446420 446422 446428 446434 446438 446440 446444 446450 446452 446458 446462 446464 446468 446470 446474 446476 446478 446479 446480 446482 446483 446484 446486 446488 446492 446494 446498 446500 446504 446510 446512 446518 446522 446524 446528 446534 446540 446542 446548 446552 446554 446560 446564 446570 446578 447348
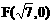 ,直线y=x-1与其相交于M、N两点,MN中点的横坐标为
,直线y=x-1与其相交于M、N两点,MN中点的横坐标为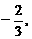 则此双曲线的方程是
则此双曲线的方程是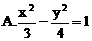
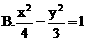
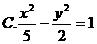
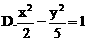

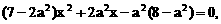
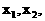 分别为点M、N的横坐标.从而MN中点的横坐标为
分别为点M、N的横坐标.从而MN中点的横坐标为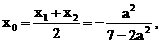
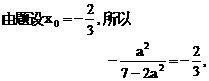
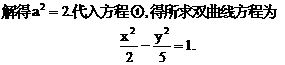
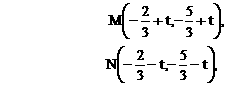
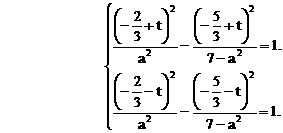
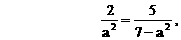

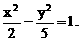
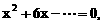
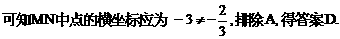
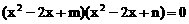 的四个根组成一个首项为
的四个根组成一个首项为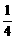 的等差数列,则|m-n|=
的等差数列,则|m-n|=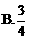
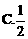
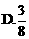
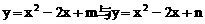 有公共的对称轴x=1,又它们与x轴的4个交点的横坐标(即题设方程的4个根)成等差数列,所以可设为
有公共的对称轴x=1,又它们与x轴的4个交点的横坐标(即题设方程的4个根)成等差数列,所以可设为

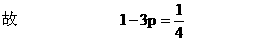
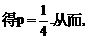
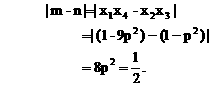
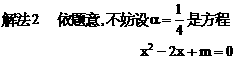



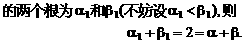
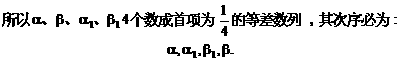
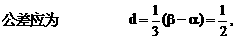
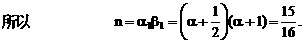
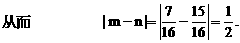
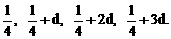
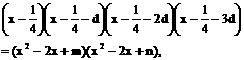
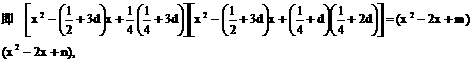
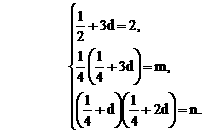

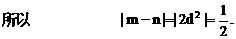
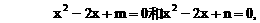
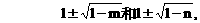
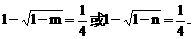
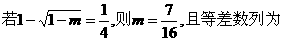

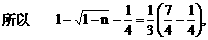
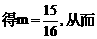
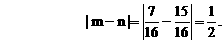

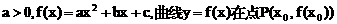 处切线的倾斜角的取值范围为
处切线的倾斜角的取值范围为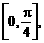 ,则点P到曲线y=f(x)对称轴距离的取值范围为
,则点P到曲线y=f(x)对称轴距离的取值范围为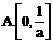
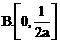
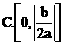
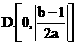
 的取值范围,进而根据曲线y=f(x)对称轴的方程,便可求得点P到对称轴距离的取值范围,如解法1.此外,也可用特殊值排除法求解.
的取值范围,进而根据曲线y=f(x)对称轴的方程,便可求得点P到对称轴距离的取值范围,如解法1.此外,也可用特殊值排除法求解.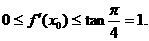
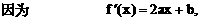
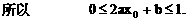
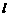 :
: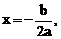
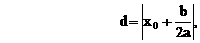

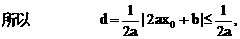

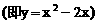 的对称轴为直线l:x=1.曲线在点P处切线的斜率为
的对称轴为直线l:x=1.曲线在点P处切线的斜率为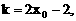
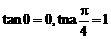 及tanx的单调性,依题设知k的取值范围为[0,1],所以
及tanx的单调性,依题设知k的取值范围为[0,1],所以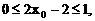
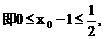 得点P到对称轴
得点P到对称轴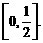 据此,可排除选项A,C,D,得答案B.
据此,可排除选项A,C,D,得答案B.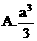
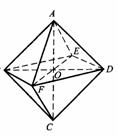
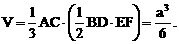
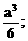 又如,由对称性,将正方体切成相等的八个小正方体,这时题没的八面体也被切成八个相等的三棱锥,每个三棱锥的体积等于小正方体的体积的
又如,由对称性,将正方体切成相等的八个小正方体,这时题没的八面体也被切成八个相等的三棱锥,每个三棱锥的体积等于小正方体的体积的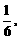 所以八面体的体积是正方体体积的
所以八面体的体积是正方体体积的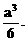
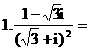
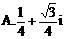
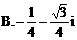
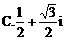
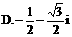
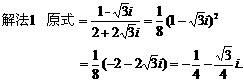
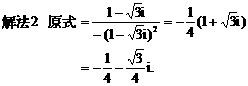
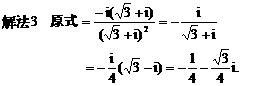
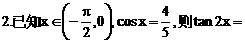
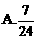
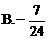
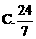
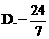
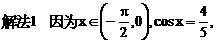
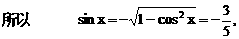
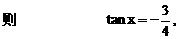
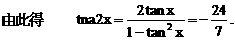
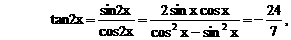
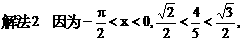
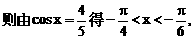
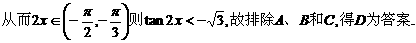
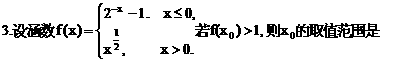
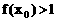 化为等价的不等式组求解,如解法1;也可用特殊值排除法求解,如解法2;还可以利用单调性,结合解方程求解,如解法3.
化为等价的不等式组求解,如解法1;也可用特殊值排除法求解,如解法2;还可以利用单调性,结合解方程求解,如解法3.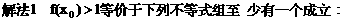
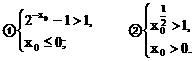
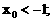 解不等式组②得
解不等式组②得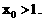 综合得
综合得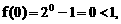 排除A和B;由f(0.04)=0.2<1,排除C,得答案D.
排除A和B;由f(0.04)=0.2<1,排除C,得答案D.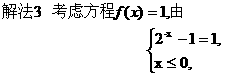

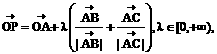
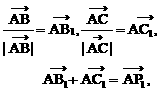
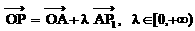
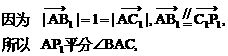
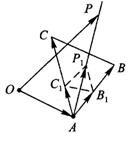
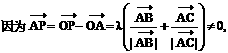
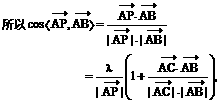
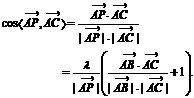
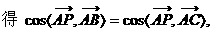
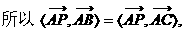
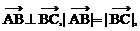 如图.
如图.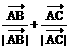 的射线
的射线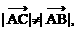 所以射线
所以射线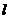 不平分BC,即不通过△ABC的重心,排除选项C.从而得选项B为答案.
不平分BC,即不通过△ABC的重心,排除选项C.从而得选项B为答案.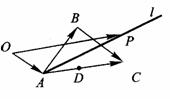
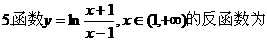
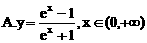

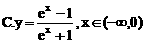


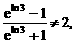
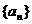 的前n项和为Sn,满足:
的前n项和为Sn,满足: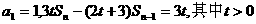 ,
,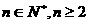
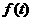 ,数列
,数列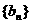 满足
满足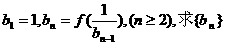 的
的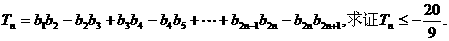
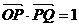 ;
;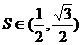 ,求向量
,求向量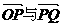 的夹角
的夹角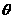 的取值范围;
的取值范围;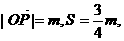 以O为中心,P为焦点的椭圆经过点Q,当
以O为中心,P为焦点的椭圆经过点Q,当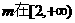 上变
上变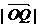 的最小值,并求出此时的椭圆方程.
的最小值,并求出此时的椭圆方程.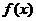 是定义在
是定义在 上的奇函数,当
上的奇函数,当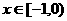 时,
时,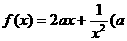 为实数)
为实数) 的解析式;
的解析式;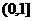 上为增函数,求a取值范围;
上为增函数,求a取值范围;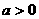 ,函数
,函数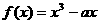 ,
,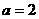 时,判断函数
时,判断函数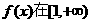 上单调性,并加以证明;
上单调性,并加以证明;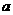 的取值范围,使
的取值范围,使 为常数,
为常数,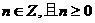 ),若产品销售价保持不变,第n次
),若产品销售价保持不变,第n次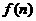 万元.
万元.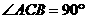 ,E、F、G
,E、F、G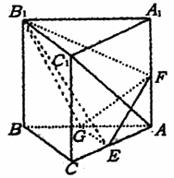 分别是AC、AA1、AB的中点.
分别是AC、AA1、AB的中点.