0 446066 446074 446080 446084 446090 446092 446096 446102 446104 446110 446116 446120 446122 446126 446132 446134 446140 446144 446146 446150 446152 446156 446158 446160 446161 446162 446164 446165 446166 446168 446170 446174 446176 446180 446182 446186 446192 446194 446200 446204 446206 446210 446216 446222 446224 446230 446234 446236 446242 446246 446252 446260 447348
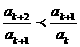 ;
; 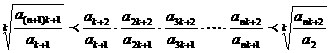 ;
; 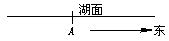 (理)在东西方向直线延伸的湖岸上有一港口A,一艘机艇以40 km/h的速度从A港出发,30分钟后因故障而停在湖里,已知机艇出发后,先按直线前进,以后又改成正北,但不知 最初的方向和何时改变的方向,如果去营救,用图示表示营救区域(提示:满足不等式y≥ax+b的点(x,y)不在y=ax+b的下方).
(理)在东西方向直线延伸的湖岸上有一港口A,一艘机艇以40 km/h的速度从A港出发,30分钟后因故障而停在湖里,已知机艇出发后,先按直线前进,以后又改成正北,但不知 最初的方向和何时改变的方向,如果去营救,用图示表示营救区域(提示:满足不等式y≥ax+b的点(x,y)不在y=ax+b的下方). 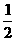 x2+6,点P(2,4),A、B在抛物线上,且直线PA、PB的倾斜角互补;
x2+6,点P(2,4),A、B在抛物线上,且直线PA、PB的倾斜角互补; 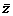 +1)=|z2|,且
+1)=|z2|,且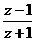 是纯虚数;
是纯虚数; 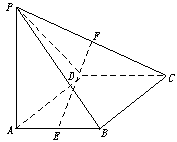 (Ⅱ)求argz.
(Ⅱ)求argz.  <1},B={x|log4(x+a)<1},若A∩B=
<1},B={x|log4(x+a)<1},若A∩B=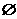 ,求实数a的取值范围.
,求实数a的取值范围.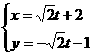 (t为参数),若以原点为极点,x轴的正半轴为极轴的极坐标系中,点P的极坐标为(-2,π),则点P到直线l的距离为______________.
(t为参数),若以原点为极点,x轴的正半轴为极轴的极坐标系中,点P的极坐标为(-2,π),则点P到直线l的距离为______________.