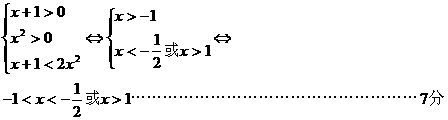
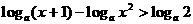0 445995 446003 446009 446013 446019 446021 446025 446031 446033 446039 446045 446049 446051 446055 446061 446063 446069 446073 446075 446079 446081 446085 446087 446089 446090 446091 446093 446094 446095 446097 446099 446103 446105 446109 446111 446115 446121 446123 446129 446133 446135 446139 446145 446151 446153 446159 446163 446165 446171 446175 446181 446189 447348
 ………………………3分
………………………3分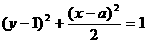 …………………………4分
…………………………4分
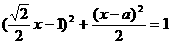
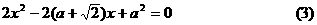 ……………………7分
……………………7分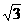 有
有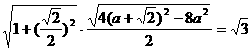 …………………………………9分
…………………………………9分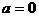 或
或 ,并且都使方程(3)有实根
,并且都使方程(3)有实根 变换后的椭圆方程为:
变换后的椭圆方程为: ………………………………11分
………………………………11分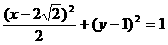 ………………………………………………12分
………………………………………………12分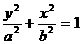

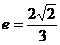 解得
解得
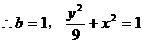 为所求………………………………………3分
为所求………………………………………3分 的方程为
的方程为
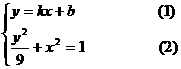
 ……………4分
……………4分


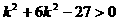 ………………………………9分
………………………………9分
 ………………………………………………………10分
………………………………………………………10分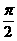
 ……………………12分
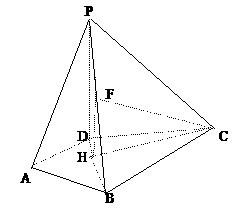
……………………12分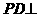 平面ABCD,BC
平面ABCD,BC 平面ABCD,得
平面ABCD,得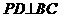 。
。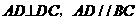 ,得
,得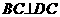 。
。 ,则
,则 平面PDC……………………2分
平面PDC……………………2分 为直线PB与平面PDC所成的角
为直线PB与平面PDC所成的角 ,则
,则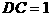 ,
, ,可求出
,可求出 。………………3分
。………………3分 。
。 中,由
中,由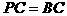 得
得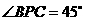
 ……………………………………4分
……………………………………4分 。
。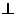 平面PDC,BC
平面PDC,BC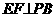 于F,连DF
于F,连DF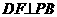
 为二面角D-PB-C的平面角…………………………………7分
为二面角D-PB-C的平面角…………………………………7分 中,求得
中,求得
 中,求得
中,求得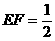
 中,
中,
 ………………………………8分
………………………………8分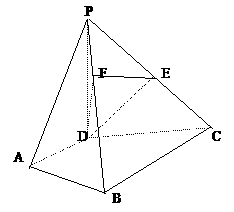
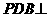 平面ABCD
平面ABCD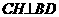 于H
于H 平面PDB…………………………………………………………5分
平面PDB…………………………………………………………5分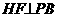 于F,连CF
于F,连CF
 为二面角D-PB-C的平面角………………………………7分
为二面角D-PB-C的平面角………………………………7分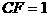
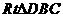 中,求出
中,求出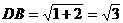 ,可进一步求出斜边上的高
,可进一步求出斜边上的高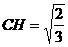
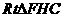 中,求出
中,求出
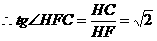
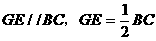
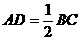
 ………………………………………………………………10分
………………………………………………………………10分 平面PBC
平面PBC 平面PBC
平面PBC 平面PAB
平面PAB

 平面PAB
平面PAB 平面PAB……………………………………………………12分
平面PAB……………………………………………………12分
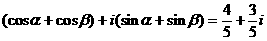
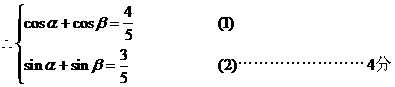

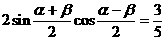 …………………………8分
…………………………8分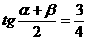 ……………………………………10分
……………………………………10分 ………………12分
………………12分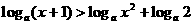
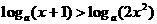 ………………………………………………2分
………………………………………………2分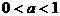 时
时
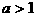 时
时

 …………………12分
…………………12分