0 446109 446117 446123 446127 446133 446135 446139 446145 446147 446153 446159 446163 446165 446169 446175 446177 446183 446187 446189 446193 446195 446199 446201 446203 446204 446205 446207 446208 446209 446211 446213 446217 446219 446223 446225 446229 446235 446237 446243 446247 446249 446253 446259 446265 446267 446273 446277 446279 446285 446289 446295 446303 447348
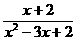 ≥1②的解集为B={x|0≤x<1或2<x≤4,x∈R}则A∩B={x|0≤x<1或2<x<3}. 4分
≥1②的解集为B={x|0≤x<1或2<x≤4,x∈R}则A∩B={x|0≤x<1或2<x<3}. 4分 C
C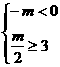 ,∴m≥6;
,∴m≥6;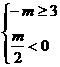 ,∴m≤-3.
,∴m≤-3.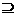 A∪B 10分
A∪B 10分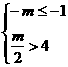 ,∴m>8;
,∴m>8;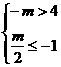 ,∴m<-4.
,∴m<-4.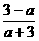 <-1, 3分
<-1, 3分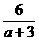 >0知
>0知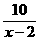 ,代入上式并整理得:
,代入上式并整理得: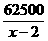 +100(x-2)≥31450+2
+100(x-2)≥31450+2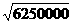 =36450(元) 10分
=36450(元) 10分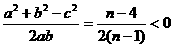 , 4分
, 4分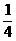 ,
,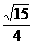 ,∴当x=2时,Smax=
,∴当x=2时,Smax= . 12分
. 12分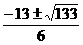 . 5分
. 5分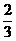 时,|ka-2b|取得最小值为2
时,|ka-2b|取得最小值为2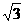 . 12分
. 12分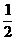 ,
,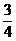 ,cos(A+B)=cos(180°-C)=cos120°=-
,cos(A+B)=cos(180°-C)=cos120°=-