高考命题注重考基础知识,考技能,反映基础知识的命题达百分之七十,但又要求有一定的难度,灵活度,综合度,这就要求复习不停留在知识的一般运用上,如函数是高考必考的内容,如2003年的高考中理解的第3、14、19,文科的第7、11、17题,理科的第6题实质也是二次函数的最值问题。这些题目体现由知识立意向能力立意转化,以知识为背景,突出能力的考查和思维的训练。要顺利解决这些问题,没有形成良好的函数,方程观点,是解决不了的。例如应用题的训练中,可以设计如图所示的思维线索
|
|

|
|

引导学生在面对新情景,新问题时,从有用信息提取入手,建立数学问题的模型,找出解决模型所需要的知识要求,方法。对得出的结果应检验。通过训练从而达到提高解决实际问题的能力。复习的最终目标毕竟要面向高考,通过复习使学生能够在心理、思维、体力等方面保持稳定、从容应对各种题目,最终取得优异成绩。
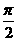 +arctgx,f(x)的反函数是f-1(x),则f-1(
+arctgx,f(x)的反函数是f-1(x),则f-1(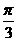 )等于
)等于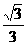 B.-
B.-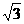 C.
C. 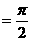 .
试求∠A、∠B、∠C的值.
.
试求∠A、∠B、∠C的值. 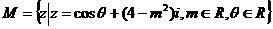 ,
,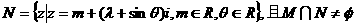 ,求实数λ的取值范围.
,求实数λ的取值范围. 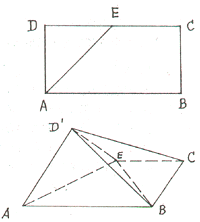 (21)(本小题满分14分)
(21)(本小题满分14分)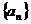 的首项a1=1,其公比q为实常数,且
的首项a1=1,其公比q为实常数,且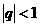 ,数列
,数列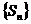 的前n项和为Tn.
的前n项和为Tn.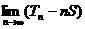 .(写成关于q的表达式)
.(写成关于q的表达式)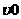 米/秒,一个匀速行进的车队有10辆车,每辆车长为l米,相邻两车之间距离m(米)与车速υ(米/秒)的平方成正比,比例系数为k,自第1辆车车头进隧道至第10辆车车尾离开隧道时所用的时间为t秒.
米/秒,一个匀速行进的车队有10辆车,每辆车长为l米,相邻两车之间距离m(米)与车速υ(米/秒)的平方成正比,比例系数为k,自第1辆车车头进隧道至第10辆车车尾离开隧道时所用的时间为t秒.
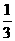 .
. 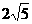 ,在x轴上方的A、B两点在一条以x轴为对称轴的抛物线上,求此抛物线的方程及直线l的方程.
,在x轴上方的A、B两点在一条以x轴为对称轴的抛物线上,求此抛物线的方程及直线l的方程. 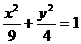 的中心O为顶点,以椭圆的左准线
的中心O为顶点,以椭圆的左准线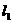 为准线的抛物线与椭圆的右准线
为准线的抛物线与椭圆的右准线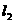 交于A、B两点,则
交于A、B两点,则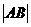 的值为 .
的值为 . 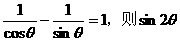 的值等于
.
的值等于
. 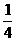 (B)
(B)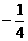 (C)
(C)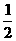 (D)
(D)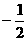
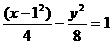 的渐近线方程是
( )
的渐近线方程是
( )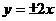 (B)
(B)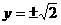 (C)
(C)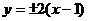 (D)
(D)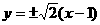
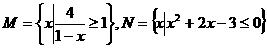 ,那么集合M与N之间的关系是
( )
,那么集合M与N之间的关系是
( )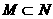 (B)M=N (C)
(B)M=N (C)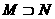 (D)
(D)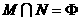
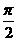 ,则实数t的值是
( )
,则实数t的值是
( )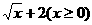 的反函数f-1(x)是图象是
( )
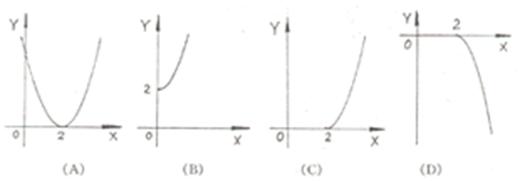
的反函数f-1(x)是图象是
( )
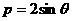 上,点B在曲线
上,点B在曲线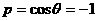 上,则
上,则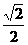 (D)1
(D)1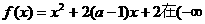 ,4]上是减函数,那么实数 a的取值范围是
( )
,4]上是减函数,那么实数 a的取值范围是
( )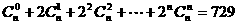 ,则
,则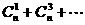 的值等于( )
的值等于( )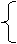 (9)理科做:直线
(9)理科做:直线 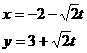 (t为参数)上到点A(-2,3)的距离等于
(t为参数)上到点A(-2,3)的距离等于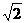 的一个点的坐标是
( )
的一个点的坐标是
( )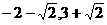 )
(D)(-3,4)
)
(D)(-3,4)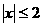 的必要但不充分条件是
( )
的必要但不充分条件是
( )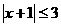 (B)
(B)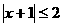 (C)
(C)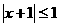 (D)
(D)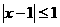
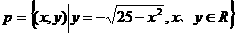 及
及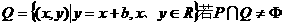 ,则实数b的取值范围是( )
,则实数b的取值范围是( )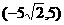 (C)
(C) (D)
(D)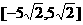
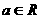 )的倾斜角的取值范围是
( )
)的倾斜角的取值范围是
( )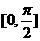 (B)[0,π]
(B)[0,π]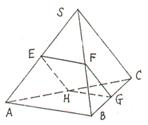 (C)
(C)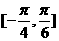 (D)
(D)