22、解:(1)由f(x)=-(cosx-a)2+a3+a2-a+1
令t=cosx,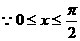 ,
0≤t≤1
,
0≤t≤1
则g(t)=-(t-a)2+a3+a2-a+1
10若a<0,则当t=0时,M(a)=g(0)=a3-a+1
20若0≤a≤1,则当t=a时,M(a)=g(a)=a3+a2-a+1
30若a>1,则当t=1时,M(a)=g(1)=a3+a
∴M(a)=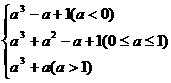
(2)当-1≤a<0时,M(a)=a3-a+1
∴M’(a)=3a2-1=3(a+ )(a-
)(a- )
)
令M’(a)=0,得a1=- ,或a2=
,或a2= (舍去)
(舍去)
且M(- )=(-
)=(- )3-(-
)3-(- )+1=
)+1= +1
+1
当0≤a<1时,M(a)=a3+a2-a+1
∴M’(a)=3a2+2a-1=(3a-1)(a+1)
令M’(a)=0,得a3= ,或a4=-1(舍去)
,或a4=-1(舍去)
且M( )=(
)=( )3+(
)3+( )2-
)2- +1=
+1=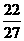
列表如下
|
a |
-1 |
(1,- ) ) |
- |
(- ,0) ,0) |
0 |
(0, ) ) |
 |
( ,1) ,1) |
1 |
|
M’(a) |
|
+ |
|
|
|
- |
|
+ |
|
|
M(a) |
1 |
|
 +1 +1 |
|
1 |
|
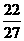 |
|
2 |
从上表可知:
当a=1时,M(a)取得最大值2
当a= 时,M(a)取得最小值
时,M(a)取得最小值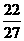 。
。
 中,
中,
 四个条件中,是
四个条件中,是 的充分且必要条件的有:( )
的充分且必要条件的有:( ) (1)由
(1)由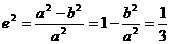 ,得
,得
 :y=x+2与圆x2+y2=b2相切,∴
:y=x+2与圆x2+y2=b2相切,∴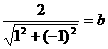 ,解得
,解得 ,则a2=3。
,则a2=3。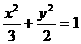 。
。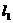 :x=-3。
:x=-3。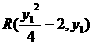 、
、 ,由QR⊥RS得
,由QR⊥RS得
 )
) ≥2×16+32=64
≥2×16+32=64 -2)+2]2+y22=
-2)+2]2+y22=
 .
.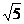 ,+∞)。
,+∞)。 (2)
(2)
 ,∴BE⊥平面PAC
,∴BE⊥平面PAC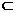 平面PBE,∴平面PBE⊥平面PAC。
平面PBE,∴平面PBE⊥平面PAC。 平面PEF,∴AD//平面PEF。
平面PEF,∴AD//平面PEF。
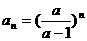 (2)
(2)
 时,A、B、C三点能构成三角形;
时,A、B、C三点能构成三角形; 时,三角形ABC为直角三角形,且∠A=90°。
时,三角形ABC为直角三角形,且∠A=90°。 ,0) 14、
,0) 14、 15、10
16、1
15、10
16、1 )
)