22、解:(Ⅰ)
|

又 
故 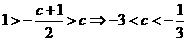 . …………………………………4分
. …………………………………4分
方程 +1=0有实根,即
+1=0有实根,即 有实根.
有实根.
故 
即 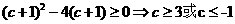 . …………………………6分
. …………………………6分
又  ,
,
得 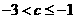 .
.
由  知
知 .
………………………………8分
.
………………………………8分
(Ⅱ)
|

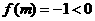 ,
,

 .
.

 .
…………………………………12分
.
…………………………………12分

 .
.

 的符号为正.
…………………………………14分
的符号为正.
…………………………………14分
21、解:(Ⅰ)法一.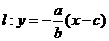 ,
,
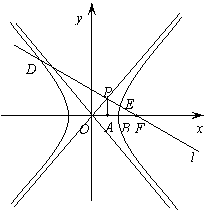
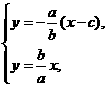 解得
解得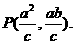 …2分
…2分

|
|
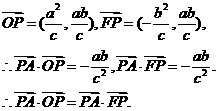
|
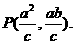
|
|

(Ⅱ)
|
|
|

18、解:(Ⅰ)方法一
由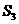 ,
,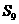 ,
,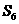 成等差数列,得
成等差数列,得 ,
………………2分
,
………………2分
若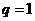 ,则
,则 ,
, ,
,
由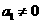 得
得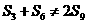 ,与题意不符,所以
,与题意不符,所以 。
……………4分
。
……………4分
由 ,得
,得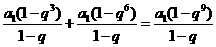 。 ………………6分
。 ………………6分
整理,得 。
。
由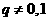 ,得
,得 。
…………………8分
。
…………………8分
(Ⅰ)方法二
由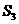 ,
,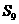 ,
,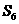 成等差数列,得
成等差数列,得 ,
…………………2分
,
…………………2分
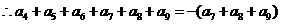 …………………4分
…………………4分
移项得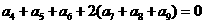
|
|

(Ⅱ) 方法一
由(1)知:
|
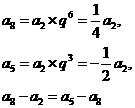
所以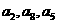 成等差数列。 …………………………………………12分
成等差数列。 …………………………………………12分
(Ⅱ) 方法二
由(1)知:
|

所以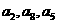 成等差数列。
…………………………………………12分
成等差数列。
…………………………………………12分
17、解: (方法一)
|
|
|
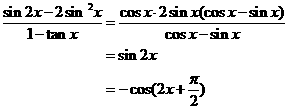
|
|

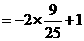
|
 .
.
(方法二)
|
|

|
|
|
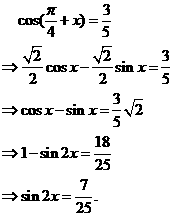
|
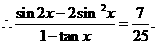
 =(cos
=(cos ,sin
,sin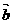 =(cos
=(cos ,-sin
,-sin ,
, ].
]. 及
及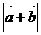 ;
;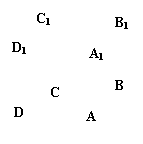 如图为一几何体的展开图:
如图为一几何体的展开图:
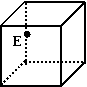
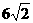 (单位:cm)
(单位:cm)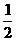 ;
; (x<-2),f(x)的反函数为g(x),点An(an,
(x<-2),f(x)的反函数为g(x),点An(an,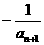 )在曲线y=g(x)上(n∈N+),且a1=1.
)在曲线y=g(x)上(n∈N+),且a1=1. }为等差数列;
}为等差数列; ,记Sn=b1+b2+……+bn,求Sn.
,记Sn=b1+b2+……+bn,求Sn. ≤f(
≤f(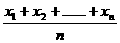 )
) B=
( )
B=
( )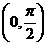 (B)
(B) (C)
(C)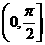 (D)
(D)
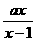 <1的解集为{x|x<1或x>2},则a=
( )
<1的解集为{x|x<1或x>2},则a=
( )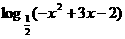 的减区间是
( )
的减区间是
( )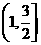 (D)
(D)
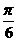 )
(B)y=sin(2x+
)
(B)y=sin(2x+ 上的任意一点,F为抛物线的焦点,点A坐标为(1,1),则|PF|+|PA|的最小值为
( )
上的任意一点,F为抛物线的焦点,点A坐标为(1,1),则|PF|+|PA|的最小值为
( ) (B)2
(C)
(B)2
(C) (D)
(D)
 (C)
(C) (D)
(D)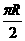
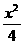 +y2=1的两焦点,P在椭圆上,当△F1PF2面积为1时,
+y2=1的两焦点,P在椭圆上,当△F1PF2面积为1时, 的值为 ( )
的值为 ( )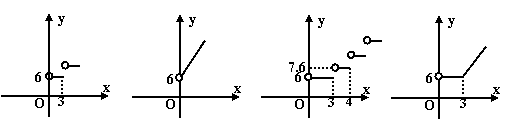
 ,则z=2x+4y的最小值为( )
,则z=2x+4y的最小值为( )
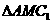 为以点M为直角顶点的等腰直角三角形,
为以点M为直角顶点的等腰直角三角形,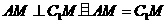 .
. ,
, 且
且 . …………………………2分
. …………………………2分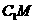 在底面内的射影为
在底面内的射影为 ,
,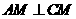 .
.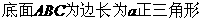 ,
,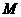 为
为 边的中点. ……………………………………………4分
边的中点. ……………………………………………4分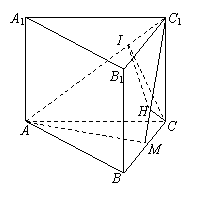 (Ⅱ) 过点
(Ⅱ) 过点 作
作 ,
,  ,
,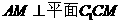
 ,
, ,
, , ……………………………………………6分
, ……………………………………………6分 ,
,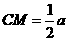 且
且 .
. .
.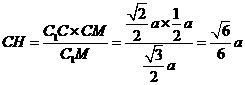 .
. 的距离为底面边长为
的距离为底面边长为 . ………………………8分
. ………………………8分 ,
,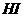 为
为 在平面
在平面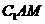 内的射影,
内的射影, ,
, 是二面角
是二面角 的平面角.……………10分
的平面角.……………10分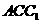 中,
中,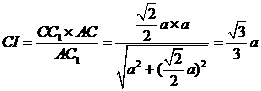 ,
, ,
,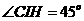 ,
, 为原点,建立如图所示的空间直角坐标系.……1分
为原点,建立如图所示的空间直角坐标系.……1分

 ,
……………………………3分
,
……………………………3分 ,
, ,
,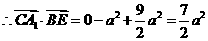 ,
, .
…………………5分
.
…………………5分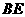 与
与 所成的角为
所成的角为 . …………………………………6分
. …………………………………6分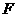 ,使
,使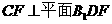 ,不妨设
,不妨设 ,
, ,
, , ……………………8分
, ……………………8分 ……………………9分
……………………9分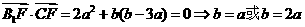 , …………………11分
, …………………11分 .………………………………12分
.………………………………12分 种,
………………………………2分
种,
………………………………2分 种. ………………………………4分
种. ………………………………4分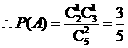 .
………………………………6分
.
………………………………6分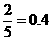 ,
,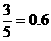 ,
……………………………8分
,
……………………………8分 .
……………………………12分
.
……………………………12分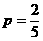 ,
……………………………10分
,
……………………………10分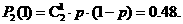 ………………………12分
………………………12分 中一组即可,如
中一组即可,如 等
等