(17)(本小题满分10分)
已知随机变量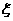 的分布列为
的分布列为
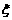 |
 |
0 |
1 |
2 |
3 |
|
P |
0.3 |
0.1 |
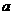 |
0.3 |
0.2 |
求实数a的值,并求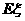 和
和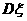 .
.
(18)(本小题满分12分)
已知函数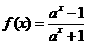
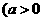 ,
,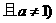 .
.
(Ⅰ)求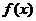 的反函数
的反函数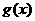 ;
;
(Ⅱ)若函数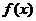 过点
过点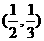 ,则函数
,则函数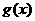 过点
过点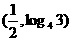 吗?为什么?
吗?为什么?
(19)(本小题满分12分)
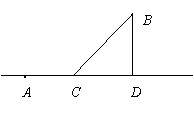
已知正三棱柱ABC-A1B1C1,底面边长AB=2,AB1⊥BC1,点O、O1分别是
 边AC、A1C1的中点,建立如图所示的空间直角坐标系.
边AC、A1C1的中点,建立如图所示的空间直角坐标系.
(Ⅰ)求正三棱柱ABC-A1B1C1的侧棱长;
(Ⅱ)求异面直线AB1与BC所成角的大小.
(20)(本小题满分12分)
如图,有甲乙两个村庄,甲村位于一直线河岸的岸边A处,乙村与甲村在河的同侧,乙村位于离河岸40km的B处,乙村到河岸的垂足D与A相距50km,两村要在此岸边合建一个自来水厂C,从自来水厂到甲村和乙村的水管费用分别为每千米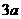 元和
元和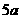 元. 现要进行工程费用测算.
元. 现要进行工程费用测算.
(Ⅰ)求出水管总费用关于水厂C到D的距离的函数
 关系式;
关系式;
(Ⅱ)问自来水厂C建在何处,才能使水管总费用最
省?
(21)(本小题满分14分)
在以O为原点的直角坐标系中,点A(3,-1)为 的直角顶点. 已知|AB|=2|OA|,且点B的纵坐标大于零.
的直角顶点. 已知|AB|=2|OA|,且点B的纵坐标大于零.
(Ⅰ)求向量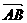 的坐标;
的坐标;
(Ⅱ)是否存在实数a,使二次函数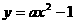 的图像上总有关于直线OB对称的两个不同的点?若不存在,说明理由;若存在,求a的取值范围.
的图像上总有关于直线OB对称的两个不同的点?若不存在,说明理由;若存在,求a的取值范围.
(22)(本小题满分14分)
若数列{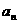 }的通项
}的通项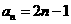 ,设数列{
,设数列{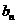 }的通项
}的通项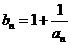 ,又记
,又记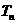 是数列{
是数列{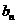 }
}
的前n项的积.
(Ⅰ)求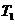 ,
,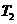 ,
,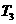 的值;
的值;
(Ⅱ)试比较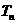 与
与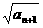 的大小,并证明你的结论.
的大小,并证明你的结论.
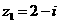 ,
,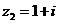 ,则
,则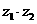 的模为__________.
的模为__________.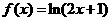 ,则
,则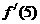 =
.
=
.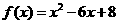
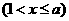 ,并且函数
,并且函数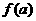 ,则实数
,则实数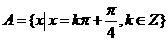 ,
,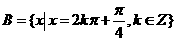 ,则有
,则有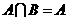 (B)
(B)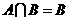 (C)
(C)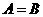 (D)
(D)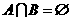
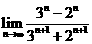 等于
等于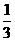 (D)
(D)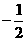
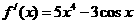 ,
, ,则
,则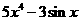 (B)
(B)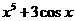 (C)
(C)
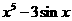 (D)
(D) 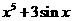
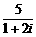 的共轭复数是
的共轭复数是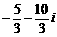 (B)
(B)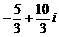 (C)
(C)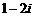 (D)
(D)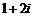
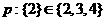 ,命题
,命题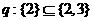 ,有如下判断:①
,有如下判断:①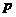 或
或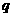 为真;②
为真;② 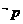 或
或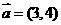 ,
,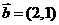 ,
,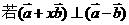 ,则x的值等于
,则x的值等于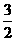 (C)3 (D)-
(C)3 (D)-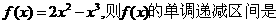
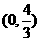 (B)
(B)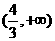 (C)
(C)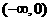 (D)
(D)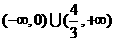
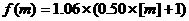 给出,其中m>0, [m]表示大于或等于m的最小整数,如:[3]=3,[3.1]=4, [3.7]=4,则从甲地到乙地通话时间为5.5分钟的电话费为
给出,其中m>0, [m]表示大于或等于m的最小整数,如:[3]=3,[3.1]=4, [3.7]=4,则从甲地到乙地通话时间为5.5分钟的电话费为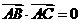 ,
,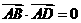 ,
,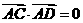 则△BCD是
则△BCD是 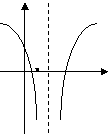
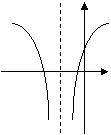 (12)函数
(12)函数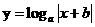 (
(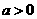 ,
,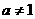 ,
,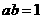 )的图象可能是
)的图象可能是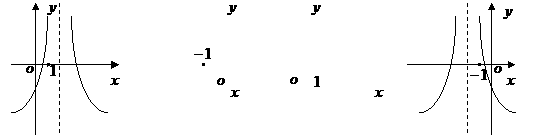 (A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)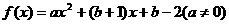 ,若存在实数
,若存在实数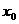 ,使
,使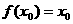 成立,则称
成立,则称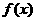 的不动点.
的不动点.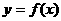 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数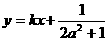 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围. 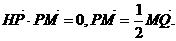
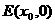 ,
,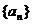 是等比数列,
是等比数列,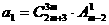 ,公比q是
,公比q是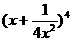 的展开式中的第二项
的展开式中的第二项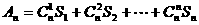 ,用n,x表示An.
,用n,x表示An.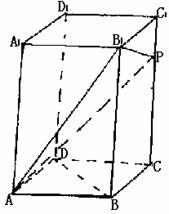
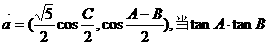
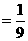 时,求
时,求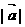 .
.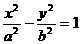 的右焦点F(c,0)的直线交双曲线于M、N两点,交y轴于P
的右焦点F(c,0)的直线交双曲线于M、N两点,交y轴于P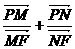 的定值为
的定值为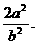 类比双曲线这一结论,在椭圆
类比双曲线这一结论,在椭圆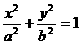 (a>b
(a>b