0 445881 445889 445895 445899 445905 445907 445911 445917 445919 445925 445931 445935 445937 445941 445947 445949 445955 445959 445961 445965 445967 445971 445973 445975 445976 445977 445979 445980 445981 445983 445985 445989 445991 445995 445997 446001 446007 446009 446015 446019 446021 446025 446031 446037 446039 446045 446049 446051 446057 446061 446067 446075 447348
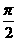 )) 被圆x2+y2=2所截的弦长为
)) 被圆x2+y2=2所截的弦长为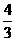
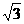 ,则m= .
,则m= . =1(a >0,b>0)的两个焦点,P为双曲线上的一点,P与F1、F2的连线互相垂直,且∠PF1F 2=15°,则双曲线的离心率为
.
=1(a >0,b>0)的两个焦点,P为双曲线上的一点,P与F1、F2的连线互相垂直,且∠PF1F 2=15°,则双曲线的离心率为
.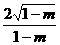 B.
B. 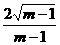
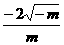 D.
D.
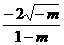
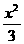 -y2=1和
-y2=1和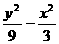 =1 B.
=1 B. 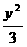 =1
D.
=1
D.  =1
=1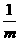 x2(m<0)的焦点坐标是( )
x2(m<0)的焦点坐标是( ) 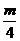 )
B.(0,-
)
B.(0,- 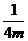 )
D.(0,-
)
D.(0,-  =1 (a>b>0)的两 个焦点把夹在两条准线间的线段三等分,那么这个椭圆的离心率是( )
=1 (a>b>0)的两 个焦点把夹在两条准线间的线段三等分,那么这个椭圆的离心率是( )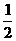 B.
B. 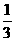 C.
C.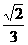 D.
D. 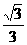
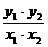 的值为( )
的值为( )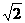 +2 B.
+2 B. 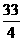 ,x=-
,x=- ,一个 焦点坐标为(6,2),则椭圆方程是( )
,一个 焦点坐标为(6,2),则椭圆方程是( ) =1 B.
=1 B. 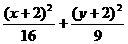 =1
=1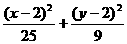 =1 D.
=1 D. 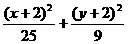 =1
=1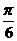 ,
,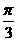 ,
,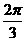 ] D.[
] D.[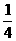 =0
B.x2+y2+x-2y+1=0
=0
B.x2+y2+x-2y+1=0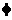 ,则实数a的取值 范围是( )
,则实数a的取值 范围是( )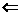 乙”,“丙是乙的充分不必要条件”,即“丙
乙”,“丙是乙的充分不必要条件”,即“丙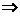 乙, 且丙
乙, 且丙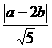 ,得
,得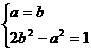 解得
解得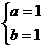 或
或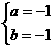
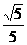 ,求该圆的方程
,求该圆的方程 (2)
(2)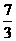 或
或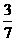 B.
B. 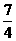 或
或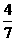 C.
C. 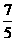 或
或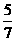 D.
D. 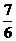 或
或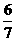
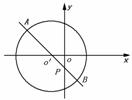
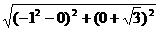 |=2
|=2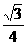 c,则双曲线的离心率为( )
c,则双曲线的离心率为( )
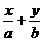 =1,
=1, 又0<a<b,双曲线中c2=a2+b2,
又0<a<b,双曲线中c2=a2+b2,
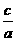 =2.
=2.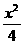 -y2 =1的两个焦点,点P在双曲线上且满足∠F1PF2=90°.则△F1PF2的面积是( )
-y2 =1的两个焦点,点P在双曲线上且满足∠F1PF2=90°.则△F1PF2的面积是( )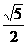 C.2
D.
C.2
D.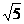
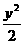 -x2=1的两个焦点坐标是
.
-x2=1的两个焦点坐标是
.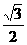 B.
B.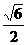 C.
C. D.2
D.2 .
.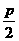 ,0),
,0),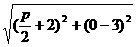
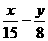 =1
=1 8x-15y-120=0
8x-15y-120=0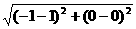 =2,得p=4.
=2,得p=4.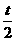 ,
,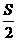 )对称;
)对称;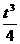 -t且t≠0.
-t且t≠0.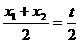 ,
,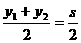 ,
,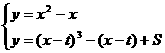 ,有且仅有一组解.
,有且仅有一组解.
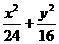 =1,直线L∶
=1,直线L∶ =1,P是L上
一点,射线OP交椭圆于R,又点Q在OP上且满足│OQ│·│OP│=│OR│2,当点P在L上移动
时,求点Q的轨迹方程,并说明轨迹是什么曲线.
=1,P是L上
一点,射线OP交椭圆于R,又点Q在OP上且满足│OQ│·│OP│=│OR│2,当点P在L上移动
时,求点Q的轨迹方程,并说明轨迹是什么曲线.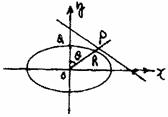
 解得
解得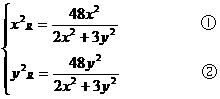
 ③,解得
③,解得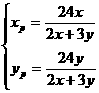 ④
④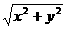 ·
·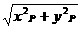
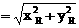 ,
,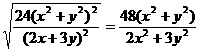 .
. =1.其中(x,y不同时为零)
=1.其中(x,y不同时为零)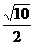 和
和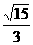 且长轴平行于x轴的椭圆.
且长轴平行于x轴的椭圆. ①
① 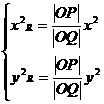 ②
②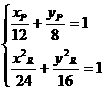 ,将(1)、(2)代
入,得
,将(1)、(2)代
入,得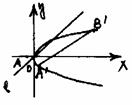
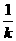 (x+1).②
(x+1).②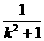 ,-
,-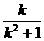 ).
).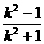 ,
,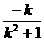 )+0=-
)+0=-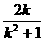 ③
③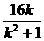 ,
,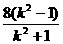 ).
).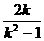 .
.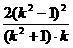 .
.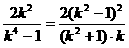 ,
,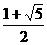 ,k2=
,k2=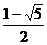 .
.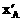 =-
=- .
.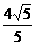 x.
x.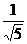 ,cosα=
,cosα=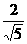 .
.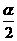 +
+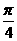 )
)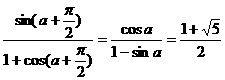 .
.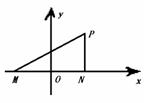
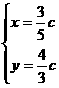 ,即P(
,即P( c,
c,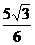 ,
,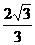 ).
).
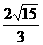 ,
,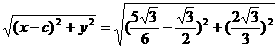
 ,a=
,a=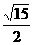 ,
,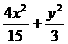 =1为所求椭圆方程.
=1为所求椭圆方程.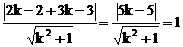

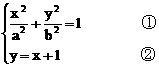

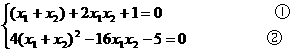
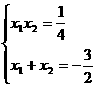 或
或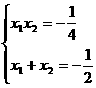
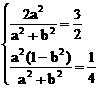 或 (Ⅱ)
或 (Ⅱ)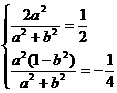
 或
或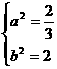
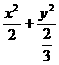 =1,或
=1,或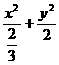 =1.
=1.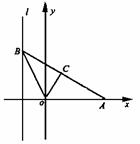
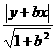 ①
①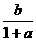 (x-a)
(x-a)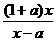 ②
② ]=[y-
]=[y-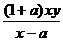 ]2
]2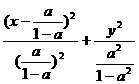 =1(0≤x<a)。
④
=1(0≤x<a)。
④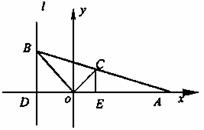
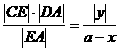 (1+a)
(1+a)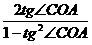 ,tg(π-∠BOD)=-tg∠BOD
,tg(π-∠BOD)=-tg∠BOD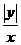 ,tg∠BOD=
(1+a)。
,tg∠BOD=
(1+a)。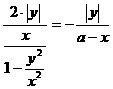 (1+a)。
(1+a)。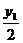 .
.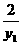 .
.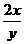 代入m的方程得-
代入m的方程得-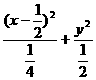 =1 (x≠1),
=1 (x≠1),
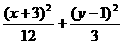 =1,∴ 对称中心是(-3,1).故选B.
=1,∴ 对称中心是(-3,1).故选B.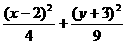 =1.
=1.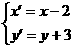 .得到新方程为
.得到新方程为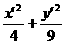 =1.
=1. =
=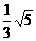 .在新坐标系中,焦点为(0,
.在新坐标系中,焦点为(0,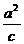 =±
=±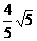
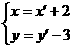 ,得在原坐标系中
,得在原坐标系中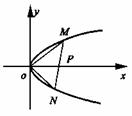
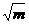 ),点N的坐标为(n,-2
),点N的坐标为(n,-2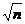 ),
),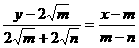
 =4
=4
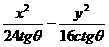 =1(
=1(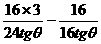 =1,tg2θ+tgθ-2=0 ,tgθ=-2,(tgθ=1舍去,因为
=1,tg2θ+tgθ-2=0 ,tgθ=-2,(tgθ=1舍去,因为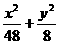 =1.
=1.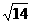 .
.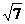 .
.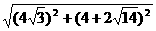
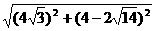
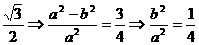 ,所以a=2b.
,所以a=2b.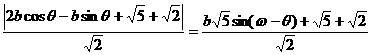 .
.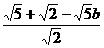 =1,则b=1,故所求椭圆方程为
=1,则b=1,故所求椭圆方程为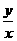 =k,则y=kx.要使k的值最大,只须直线y=kx在第一象限与圆相切
,而圆心(2,0)到直线y=kx的距离为
=k,则y=kx.要使k的值最大,只须直线y=kx在第一象限与圆相切
,而圆心(2,0)到直线y=kx的距离为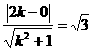 ,解得k=
,解得k=