0 445900 445908 445914 445918 445924 445926 445930 445936 445938 445944 445950 445954 445956 445960 445966 445968 445974 445978 445980 445984 445986 445990 445992 445994 445995 445996 445998 445999 446000 446002 446004 446008 446010 446014 446016 446020 446026 446028 446034 446038 446040 446044 446050 446056 446058 446064 446068 446070 446076 446080 446086 446094 447348
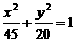 的两个焦点为F1、F2,P为椭圆上一点,且PF1⊥PF2,则||PF1|-|PF2||=_________.
的两个焦点为F1、F2,P为椭圆上一点,且PF1⊥PF2,则||PF1|-|PF2||=_________.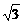 ,0),P为圆上任一点,则PQ的中垂线与OP之交点M轨迹为(O为原点)
,0),P为圆上任一点,则PQ的中垂线与OP之交点M轨迹为(O为原点)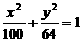
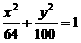
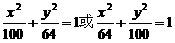
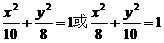
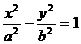 的离心率
的离心率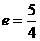 , 半虚轴长为2, 求双曲线方程.
, 半虚轴长为2, 求双曲线方程.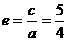 , 可令a=4k, c=5k, 则b2=c2-a2=9k2=4,
, 可令a=4k, c=5k, 则b2=c2-a2=9k2=4,
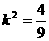 .于是
.于是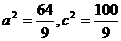 ,
, 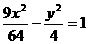 .翰林汇
.翰林汇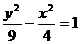 的以点P(a,1)为中点的弦所在直线方程,并讨论a取怎样的值时这样的弦才存在.
的以点P(a,1)为中点的弦所在直线方程,并讨论a取怎样的值时这样的弦才存在.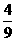 ax-
ax-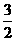 <a<
<a< 或a<-
或a<-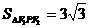 ,求∠F1PF2的大小.
,求∠F1PF2的大小.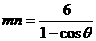 ,
, 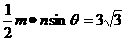 ,
, 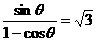 , 最后得
, 最后得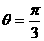 .翰林汇
.翰林汇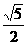 ,若点P(0,5)到双曲线上的点的距离的最小值是2时,求双曲线的方程.翰林汇
,若点P(0,5)到双曲线上的点的距离的最小值是2时,求双曲线的方程.翰林汇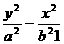 ;M(x,y)为双曲线上任意一点.
;M(x,y)为双曲线上任意一点.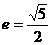 ,∴
,∴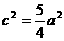 ,∴b2=c2-a2=
,∴b2=c2-a2=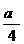 .
.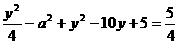 (y-4)2+5-a2.
(y-4)2+5-a2.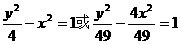
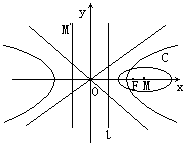
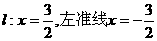 , 再设P(x,y)在C上,
, 再设P(x,y)在C上, 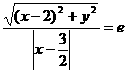 , 得(1-e2)x2+y2+(3e2-4)x+4-
, 得(1-e2)x2+y2+(3e2-4)x+4-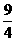 e2=0,
e2=0, 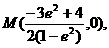
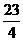 =0,
=0,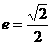
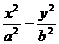 =1上,F1、F2是左右焦点,O为原点,
=1上,F1、F2是左右焦点,O为原点,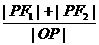 的取值范围.
的取值范围. =1,
=1,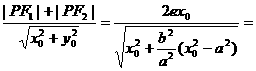
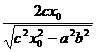 ,
,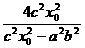 ,解得
,解得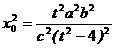
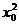 ≥a2,
≥a2,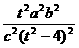 ≥a2 ∴
≥a2 ∴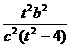 ≥1 ∴
≥1 ∴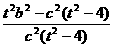 ≥0,由此得:
≥0,由此得: 解得2<t≤2e
解得2<t≤2e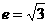 ,一条准线的方程为
,一条准线的方程为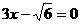 ,求此双曲线的标准方程.
,求此双曲线的标准方程. 解得
解得 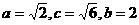 .
.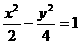 .翰林汇
.翰林汇