0 445882 445890 445896 445900 445906 445908 445912 445918 445920 445926 445932 445936 445938 445942 445948 445950 445956 445960 445962 445966 445968 445972 445974 445976 445977 445978 445980 445981 445982 445984 445986 445990 445992 445996 445998 446002 446008 446010 446016 446020 446022 446026 446032 446038 446040 446046 446050 446052 446058 446062 446068 446076 447348
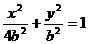 上一点P到右准线的距离是2
上一点P到右准线的距离是2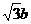 ,则该点到椭圆左焦点的距离是……( )
,则该点到椭圆左焦点的距离是……( )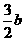 (C)
(C)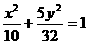 的两个顶点,双曲线的两条准线分别通过椭圆的两个焦点,则此双曲线的方程是……………………………………………………………………( )
的两个顶点,双曲线的两条准线分别通过椭圆的两个焦点,则此双曲线的方程是……………………………………………………………………( )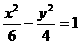 (B)
(B)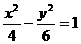 (C)
(C)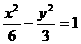 (D)
(D)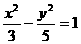
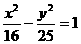 的两条渐近线所夹的锐角是………………………………………………( )
的两条渐近线所夹的锐角是………………………………………………( )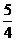 (B)π-arctan
(B)π-arctan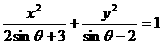 所表示的图形是………………………………………………( )
所表示的图形是………………………………………………( )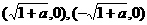 (B)
(B)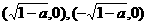
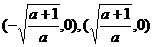 (D)
(D)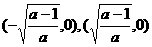
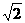 (B)2
(C)2或
(B)2
(C)2或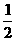 (D)
(D)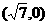 和定直线
和定直线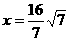 的距离之比为
的距离之比为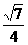 的动点轨迹方程是…………………( )
的动点轨迹方程是…………………( )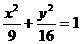 (B)
(B)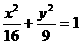 (C)
(C)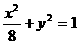 (D)
(D)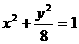
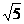 、离心率为
、离心率为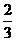 的椭圆的两个焦点分别为F1、F2,过F1作直线交椭圆于A、B两点,则△ABF2的周长为………………………………………………………………………………( )
的椭圆的两个焦点分别为F1、F2,过F1作直线交椭圆于A、B两点,则△ABF2的周长为………………………………………………………………………………( ) =1上一点P与两焦点 F1F2连线所成的角∠F1PF2=α,求△F1PF2的面积;
=1上一点P与两焦点 F1F2连线所成的角∠F1PF2=α,求△F1PF2的面积; =1 ,求△F1PF2的面积.
=1 ,求△F1PF2的面积. 的直线交两条准线于M、N,以MN为直径的圆过原点,求双曲线的方程.
的直线交两条准线于M、N,以MN为直径的圆过原点,求双曲线的方程.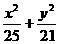 =1,左、右焦点分别为 F2、F1,右准线为L,问能否在椭圆上求得一点P,使│PF1│是P到L的距离d与│PF2│的比例中项?若能,求出P点坐标,若不能,说明理由.
=1,左、右焦点分别为 F2、F1,右准线为L,问能否在椭圆上求得一点P,使│PF1│是P到L的距离d与│PF2│的比例中项?若能,求出P点坐标,若不能,说明理由. +(k-2)y2=1+k所表 示曲线的形状.
+(k-2)y2=1+k所表 示曲线的形状.