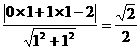0 445886 445894 445900 445904 445910 445912 445916 445922 445924 445930 445936 445940 445942 445946 445952 445954 445960 445964 445966 445970 445972 445976 445978 445980 445981 445982 445984 445985 445986 445988 445990 445994 445996 446000 446002 446006 446012 446014 446020 446024 446026 446030 446036 446042 446044 446050 446054 446056 446062 446066 446072 446080 447348
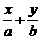 =1表示
=1表示 ,-
,- ,所得直 线的方程是x-y-2=0,若将它继续为转90°-α,所得直线的方程2x+y-1=0,则直线l的方程为
.
,所得直 线的方程是x-y-2=0,若将它继续为转90°-α,所得直线的方程2x+y-1=0,则直线l的方程为
.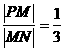 ,则点P的坐标是( )
,则点P的坐标是( )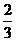 ]
B.a≠-
]
B.a≠-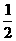
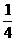 ,则θ等于( )
,则θ等于( )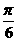 B.
B. 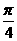 C.
C. 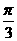 D.
D. 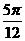
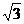 D.2
D.2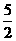 ,1]
B.[-1,
,1]
B.[-1, 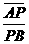 因为
因为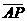 与
与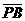 的方向相反,且|
的方向相反,且|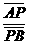 |<-1,
|<-1,
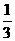 ,b=6
B.a=
,b=6
B.a=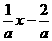 .
.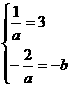 ,解得
,解得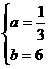
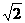 -1)x+2
-1)x+2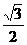 -1) x+2
-1) x+2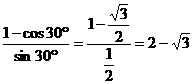 .
.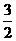 B.-2 C. -3 D.3
B.-2 C. -3 D.3 y=-
y=-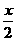 +
+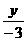 =1,
=1,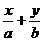 =1,
=1,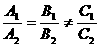
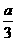 =
=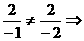 a=- 6.
a=- 6.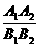 =-1
D.
=-1
D.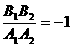
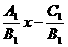 ,y=-
,y=-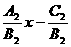 ,得k1=-
,得k1=-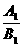 ,k2=-
,k2=-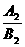 ,
,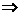 k1·k2=-1
k1·k2=-1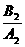
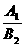 )·(
)·(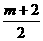 ,
,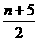 )在y=-x上,且KPQ·(-1)=-1.
)在y=-x上,且KPQ·(-1)=-1.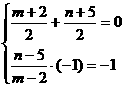 ,解得
,解得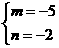
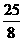 ,
,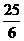 )
)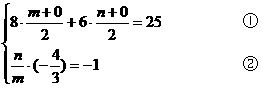
 C.1+
C.1+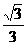 D.2-
D.2-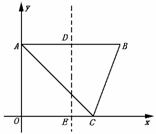
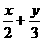 =1,即3x+ 2y=6.
=1,即3x+ 2y=6.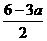 )
) 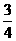 a2
(1)
a2
(1)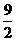 ,
,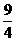 , (2)
, (2)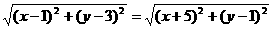 ,化简得3x+y+4= 0.
,化简得3x+y+4= 0.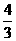 ,
,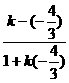 │=│
│=│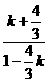 │=│
│=│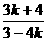 │,
│,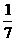 ,7
,7