0 445888 445896 445902 445906 445912 445914 445918 445924 445926 445932 445938 445942 445944 445948 445954 445956 445962 445966 445968 445972 445974 445978 445980 445982 445983 445984 445986 445987 445988 445990 445992 445996 445998 446002 446004 446008 446014 446016 446022 446026 446028 446032 446038 446044 446046 446052 446056 446058 446064 446068 446074 446082 447348
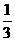 S·h,求出h即为所求.这种方法的优点是不必作出垂线即可求点面距离.难点在于如何构造合适的三棱锥以便于计算.
S·h,求出h即为所求.这种方法的优点是不必作出垂线即可求点面距离.难点在于如何构造合适的三棱锥以便于计算.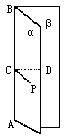
 α.
α. α,P∈β,β∥α,P∈a,a∥α,则a
α,P∈β,β∥α,P∈a,a∥α,则a α,a⊥b .
α,a⊥b .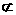 α,b
α,b α∥β.
α∥β.