例1:下列对应是不是从A到B的映射?是不是函数?
(1)A=(-∞,+∞),B=(0,+∞), f∶x→y=|x|
(2)A={x|x≥0}, B=R, f∶x→y, y2=x.
(3)A={x|x≥2, x∈Z}, B={y|y≥0, y∈Z}, f∶x→y=x2-2x+2.
(4)A={平面α内的矩形},B={平面α内的圆},f∶作矩形的外接圆。
[探路]
按映射的特点:A中每一元素都有象,且象唯一来判别;按函数的特点;A、B都是非空数集的映射来
判别。
[解]
(1)不是映射,因为0∈A,但|0|=0∈B,当然,(1)更不是函数。
(2)不是映射,更不是函数。因为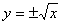 ,当x>0时,元素x的象不唯一。
,当x>0时,元素x的象不唯一。
(3)是映射。因为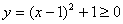 ,又当x∈A时,y∈Z,所以(3)是映射。又因为A、B都是数集,
,又当x∈A时,y∈Z,所以(3)是映射。又因为A、B都是数集,
所以(3)也是函数。
(4)是映射。因为每一个矩形都有唯一的外接圆,即A中每一元素在B中都有唯一的象,所以
(4)是映射。但A、B不是数集,所以不是函数。
例2:已知映射f∶A→B,其中,集合A={-3,-2,-1,1,2,3,4},集合B的元素都是A中元素在映射f下
的象,且对任意的a∈A,在B中和它对应的元素是|a|,则集合B中元素的个数是( )
A、4 B、5 C、6 D、7
[探路]该映射是函数,问题化为求函数的值域。
[解]已知映射f∶A→B是函数
f(x)=|x|,定义域A={-3,-2,-1,1,2,3,4},且B是值域,求值域,得
B={3,2,1,4},其元素的个数是4,因此,选A。
[评注]
用映射的概念来深刻理解函数,反之,用函数的方法来解映射的问题,这是把概念与操作相结合的现
代观点,在本例,用具体的函数来操作映射是最快的算法,而不在概念中兜圈子。
例3:已知函数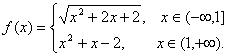
求f[f(1)]和f[f(-1)]的值。
[探路]分段计算。
[解]∵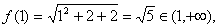
∴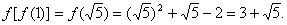
∵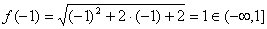
∴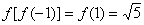
例4:下列哪组函数是同一函数?为什么?
①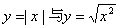
②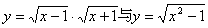
③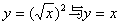
④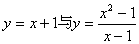
[解]
①是同一函数,因为对应法则等价: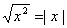 。
。
②不是同一函数,因为定义域不相等:前一函数的定义域是[1,+∞]后一函数的定义域是
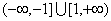 。
。
③不是同一函数,因为定义域不相等:前一函数的定义域是[0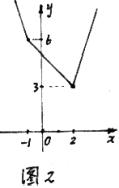 ,+∞);后一函数的定义域是
,+∞);后一函数的定义域是
(-∞,+∞)。本题也可按值域不相等直接看出。
④不是同一函数。因为定义域不相等:前一函数的定义域为R;后一函数定义
域为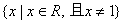 。
。
例5:作出函数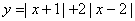 的图象。
的图象。
[探路]
先把函数化为分段函数,再画图
[解]已知函数化为
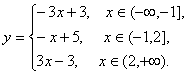
其图象如图2。
[评注]
这类函数的图象是折线,因此,还有画图快法:先求折点,即各绝对值等于零的点,如本题折点有
两个:(-1,6)、(2,3);再求一两个适当点画两边的射线,连折点间的线段,即成图。
例6:设集合A={a1,a2,a3},B={b1,b2},
(1)从A到B的映射有多少个?
(2)从B到A的映射有多少个?
[探路]
根据“什么叫映射”来做一个映射:先算每一元素的象有几种可能,然后就能算出共能做出多少个不
同的映射。
[解]
(1)作a1的象有b1或b22种方法,同样作a2,a3的象也各有2种方法,所以从A到B的映射,
共有2×2×2=8个。
(2)从B到A的映射共有3×3=9个。
例7:《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过800元的部分不必纳税,
超过800元的部分为全月应纳税所得额。此项税款按下表分段累进计算。
|
全月应纳税所得额 |
税率 |
|
不超过500元的部分 |
5% |
|
超过500元至2000元的部分 |
10% |
|
超过2000元至5000元的部分 |
15% |
|
|
|
(1)某人今年十月份工薪为4000元,问他应纳税多少元?
(2)某人去年十月份纳税26.78元,问他去年十月份的工薪为多少元?
[探路]利用分段函数进行计算。
[解](1)该人全月纳税所得额为
4000元-800元=3200元
他应纳税:500元×5%+1500元×10%+1200元×15%=355元。
(2)工薪1300元应纳税:500元×5%=25元;
工薪2800元应纳税:25元+1500元×10%=175元。
∵26.78∈(25,175),
∴他去年十月份的工薪为1300元+(26.78-25)元×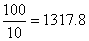 元。
元。
例8:将长为l厘米的铁丝折成矩形,问怎样折才能使矩形的面积最大?并求出这个最大面积。
[探路]选取自变量,建立面积函数,注意定义域,求出值域,便得最大值。
[解]设折成的矩形的一边长为xcm,面积为Scm2,
则 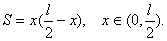
当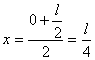 时,取得
时,取得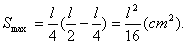
∴将铁丝折成边长为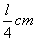 的正方形时,面积最大,最大面积为
的正方形时,面积最大,最大面积为
[评注]这种解决应用问题的方法叫“目标函数法”,其步骤是:
1、选取自变量,并确定定义域;
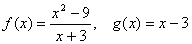

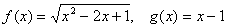
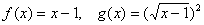
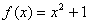 ,则f[f(-1)] 的值等于( )
,则f[f(-1)] 的值等于( )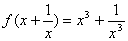 ,求f(x)和f(-3)。
,求f(x)和f(-3)。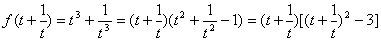
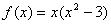
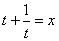 ,解出t”是不好的,请你试试看。
,解出t”是不好的,请你试试看。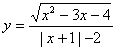 ; (2)
; (2)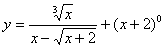
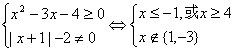
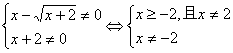
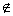 {1,-3}是最好的。
{1,-3}是最好的。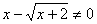 时,先解方程
时,先解方程 ,经检验x=-1是增根,应舍去。
,经检验x=-1是增根,应舍去。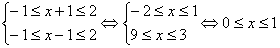 ,
,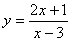 的值域。
的值域。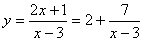
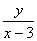 ≠0(即
≠0(即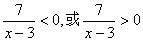 )
)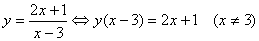
 ①
① y≠2,
y≠2,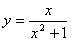 的值域。
的值域。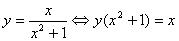
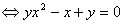 ①
①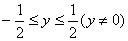 。
。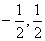 ]。
]。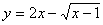 的值域。
的值域。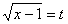 ,则x可用t的有理式表示,从而化为二次函数的值域问题。
,则x可用t的有理式表示,从而化为二次函数的值域问题。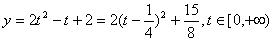
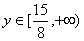
 )。
)。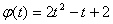 ,t∈[0,+∞],否则,换元不等
,t∈[0,+∞],否则,换元不等