0 445934 445942 445948 445952 445958 445960 445964 445970 445972 445978 445984 445988 445990 445994 446000 446002 446008 446012 446014 446018 446020 446024 446026 446028 446029 446030 446032 446033 446034 446036 446038 446042 446044 446048 446050 446054 446060 446062 446068 446072 446074 446078 446084 446090 446092 446098 446102 446104 446110 446114 446120 446128 447348
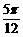 ,-
,-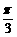 ],则y= tan(x+
],则y= tan(x+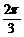 )-tan(x+
)-tan(x+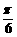 )+cos(x+
)+cos(x+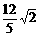 (B)
(B) (C)
(C)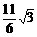 (D)
(D)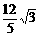
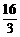 (B)
(B) (C)
(C) (D)8
(D)8
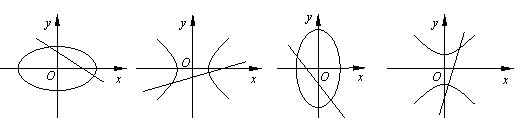
 (A)
(B)
(C) (D)
(A)
(B)
(C) (D)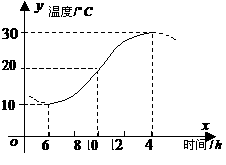
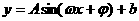 。
。 的两处同时运动。甲第1分钟走2
的两处同时运动。甲第1分钟走2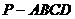 的底面是边长为
的底面是边长为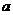 的正方形,
的正方形,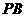
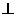 面
面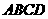 。
。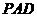 与面
与面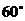 ,求这个四棱锥的体积;
,求这个四棱锥的体积; 所成的二面角恒大于
所成的二面角恒大于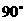 。
。
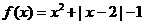 ,
,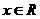 。
。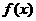 的奇偶性;
的奇偶性;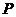 到两个定点
到两个定点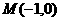 、
、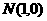 距离的比为
距离的比为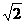 ,点
,点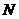 到直线
到直线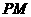 的距离为1。求直线
的距离为1。求直线 的方程。
的方程。
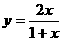
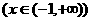 图象与其反函数图象的交点坐标为 。
图象与其反函数图象的交点坐标为 。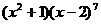 的展开式中
的展开式中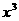 项的系数是
。
项的系数是
。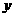 轴上;2焦点在
轴上;2焦点在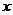 轴上;3抛物线上横坐标为1的点到焦点的距离为
轴上;3抛物线上横坐标为1的点到焦点的距离为 ;
;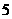 ;5由原点向过焦点的某条直线作垂线,垂足坐标为
;5由原点向过焦点的某条直线作垂线,垂足坐标为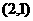 。
。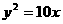 的条件是 。(要求填写合适条件的序号)
的条件是 。(要求填写合适条件的序号) 与圆
与圆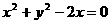 相切,则
相切,则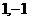 (B)
(B)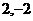 (C)
(C)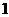 (D)
(D)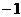
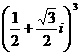 的值是
的值是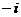 (B)
(B)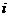 (C)
(C)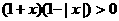 的解集是
的解集是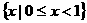 (B)
(B)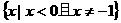 (C)
(C)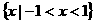 (D)
(D)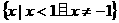
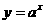 在
在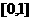 上的最大值与最小值的和为3,则
上的最大值与最小值的和为3,则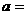
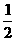 (B)
(B)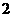 (C)
(C)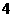 (D)
(D)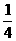
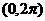 内,使
内,使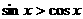 成立的
成立的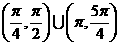 (B)
(B)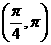 (C)
(C)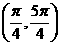 (D)
(D)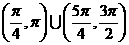
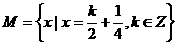 ,
,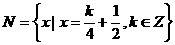 ,则
,则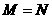 (B)
(B)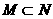 (C)
(C)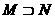 (D)
(D)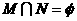
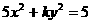 的一个焦点是
的一个焦点是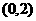 ,那么
,那么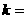
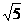 (D)
(D)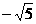
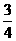 (B)
(B) (C)
(C)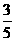 (D)
(D)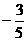
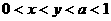 ,则有
,则有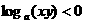 (B)
(B)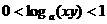 (C)
(C)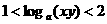 (D)
(D)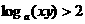
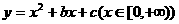 是单调函数的充要条件是
是单调函数的充要条件是 (B)
(B)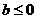 (C)
(C)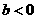 (D)
(D)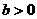
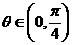 ,则二次曲线
,则二次曲线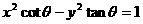 的离心率的取值范围为
的离心率的取值范围为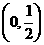 (B)
(B)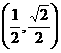 (C)
(C)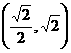 (D)
(D)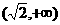
 ,
,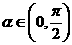 。求
。求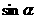 、
、 的值。
的值。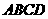 、
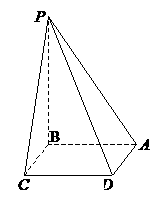
、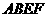 的边长都是1,而且平面
的边长都是1,而且平面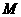
 上移动,点
上移动,点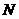 在
在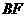 上移动,若
上移动,若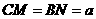
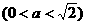 。
。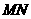 的长;
的长;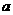 为何值时,
为何值时,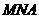 与面
与面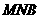 所成的二面角
所成的二面角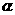 的大小。
的大小。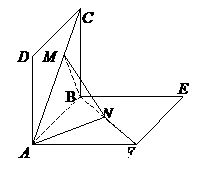
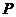 到点
到点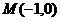 、
、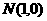 距离之差为
距离之差为 ,到
,到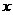 轴、
轴、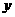 轴距离之比为
轴距离之比为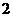 。
。 的取值范围。
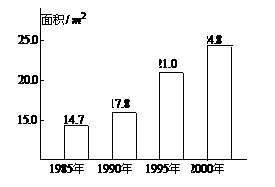
的取值范围。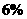 ,并且每年新增汽车数量相同。为保护城市环境,要求该城市汽车保有量不超过
,并且每年新增汽车数量相同。为保护城市环境,要求该城市汽车保有量不超过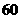 万量,那么每年新增汽车数量不应超过多少辆?
万量,那么每年新增汽车数量不应超过多少辆?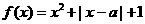 ,
,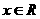 。
。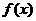 的奇偶性;
的奇偶性;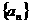 满足
满足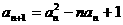 ,
,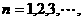
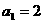 时,求
时,求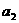 ,
,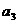 ,
,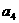 ,并由此猜想出
,并由此猜想出 的一个通项公式;
的一个通项公式;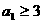 时,证明对所有的
时,证明对所有的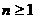 ,有
,有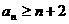 ;
;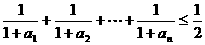 。
。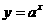 在
在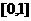 上的最大值与最小值的和为3,则
上的最大值与最小值的和为3,则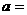 。
。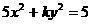 的一个焦点是
的一个焦点是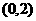 ,那么
,那么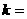 。
。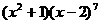 的展开式中
的展开式中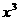 项的系数是
。
项的系数是
。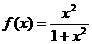 ,那么
,那么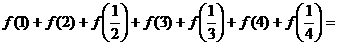 。
。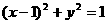 的圆心到直线
的圆心到直线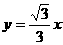 的距离是
的距离是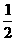 (B)
(B)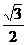 (C)
(C)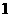 (D)
(D)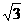
 的值是
的值是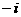 (B)
(B)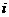 (C)
(C)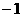 (D)
(D)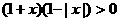 的解集是
的解集是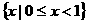 (B)
(B)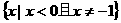 (C)
(C)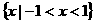 (D)
(D)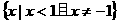
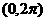 内,使
内,使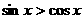 成立的
成立的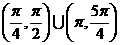 (B)
(B)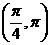 (C)
(C)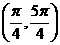 (D)
(D)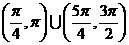
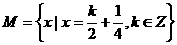 ,
,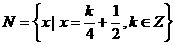 ,则
,则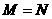 (B)
(B)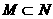 (C)
(C)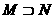 (D)
(D)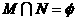
 到曲线
到曲线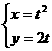 (其中参数
(其中参数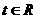 )上的点的最短距离为
)上的点的最短距离为 (B)
(B)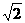 (D)
(D)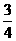 (B)
(B)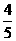 (C)
(C)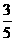 (D)
(D)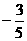
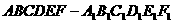 的底面边长为
的底面边长为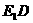 与
与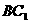 所成的角是
所成的角是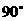 (B)
(B)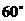 (C)
(C)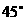 (D)
(D)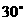
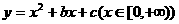 是单调函数的充要条件是
是单调函数的充要条件是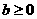 (B)
(B)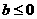 (C)
(C)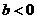 (D)
(D)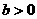
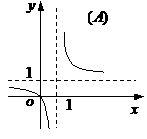
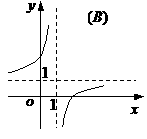
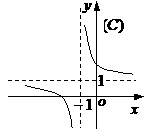
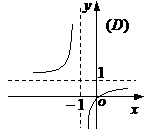
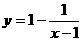 的图象是
的图象是