5.坐标变换
坐标变换 在解析几何中,把坐标系的变换(如改变坐标系原点的位置或坐标轴的方向)叫做 坐标变换.实施坐标变换时,点的位置,曲线的形状、大小、位置都不改变,仅仅只改变点 的坐标与曲线的方程.
坐标轴的平移 坐标轴的方向和长度单位不改变,只改变原点的位置,这种坐标系的变换叫 做坐标轴的平移,简称移轴.
坐标轴的平移公式 设平面内任意一点M,它在原坐标系xOy中的坐标是(x,y),在新坐标系x ′O′y′中的坐标是(x′,y′).设新坐标系的原点O′在原坐标系xOy中的坐标是(h,k),则
(1)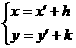 或
(2)
或
(2)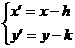
公式(1)或(2)叫做平移(或移轴)公式.
中心或顶点在(h,k)的圆锥曲线方程
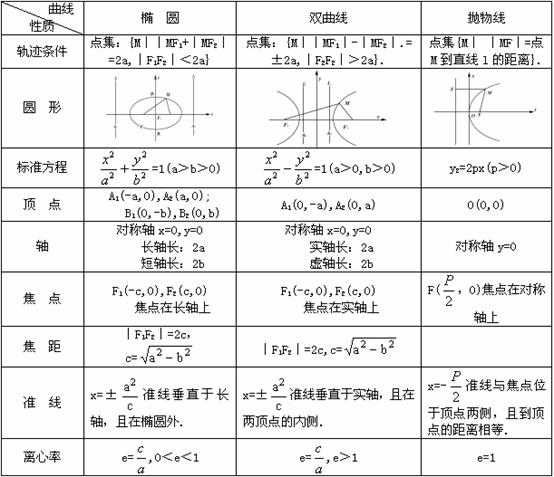
中心或顶点在(h,k)的圆锥曲线方程见下表.
|
方 程 |
焦 点 |
焦 线 |
对称轴 |
|
|
椭 圆 |
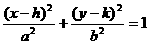 |
(±c+h,k) |
x=±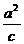 +h +h |
x=h y=k |
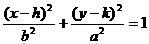 |
(h,±c+k) |
y=±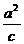 +k +k |
x=h y=k |
|
|
双曲线 |
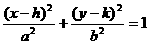 |
(±c+h,k) |
y=±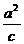 +k +k |
x=h y=k |
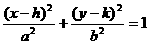 |
(h,±c+k) |
y=±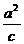 +k +k |
x=h y=k |
|
|
抛物线 |
(y-k)2=2p(x-h) |
(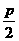 +h,k) +h,k) |
x=-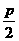 +h +h |
y=k |
|
(y-k)2=-2p(x-h) |
(-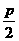 +h,k) +h,k) |
x=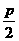 +h +h |
y=k |
|
|
(x-h)2=2p(y-k) |
(h, 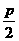 +k) +k) |
y=-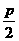 +k +k |
x=h |
|
|
(x-h)2=-2p(y-k) |
(h,- 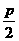 +k) +k) |
y=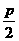 +k +k |
x=h |
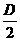 ,-
,-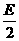 ),半径是
),半径是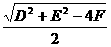 .配方,将方程x2+y2+Dx+Ey+F=0化为
.配方,将方程x2+y2+Dx+Ey+F=0化为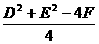
 点M在圆C内,
点M在圆C内,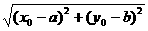 .
.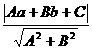 与半径r的大小关系来判定.
与半径r的大小关系来判定.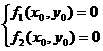
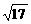 ,求l的倾斜角;
,求l的倾斜角;