0 445849 445857 445863 445867 445873 445875 445879 445885 445887 445893 445899 445903 445905 445909 445915 445917 445923 445927 445929 445933 445935 445939 445941 445943 445944 445945 445947 445948 445949 445951 445953 445957 445959 445963 445965 445969 445975 445977 445983 445987 445989 445993 445999 446005 446007 446013 446017 446019 446025 446029 446035 446043 447348
 函数
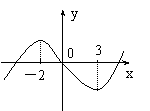
函数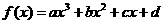 图象如右图,则函数
图象如右图,则函数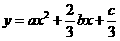 的单调递增区间为( )
的单调递增区间为( )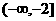 B、
B、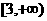
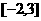 D、
D、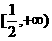
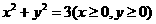 与函数
与函数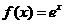 和
和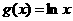 分别交于
分别交于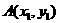 ,
,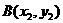 两点,则
两点,则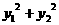 的值为( )
的值为( )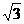 D、3
D、3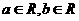 ,且ab<0,则
,且ab<0,则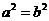 是复数
是复数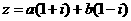 为纯虚数的( )
为纯虚数的( )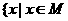 或
或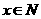 且
且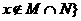 ,则(M+N)+N等于( )
,则(M+N)+N等于( ) B、
B、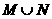 C、M D、N
C、M D、N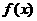 的最小值为0且有
的最小值为0且有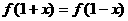 ,直线
,直线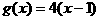 被
被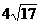 ,数列
,数列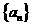 满足
满足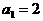 ,
,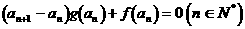 .
.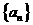 的通项公式;
的通项公式;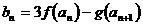 ,求数列
,求数列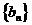 的最值及相应的n。
的最值及相应的n。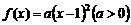 ,则直线
,则直线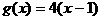 与
与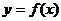 图象的两个交点为(1,0),
图象的两个交点为(1,0),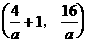 ………………………2分
………………………2分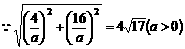
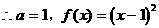 …………………4分
…………………4分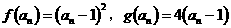
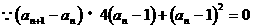
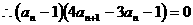
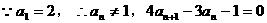 …………6分
…………6分
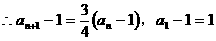 数列
数列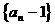 是首项为1,公比为
是首项为1,公比为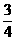 的等比数列…………8分
的等比数列…………8分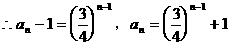 …………9分
…………9分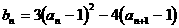
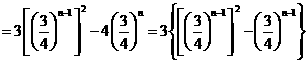 令
令 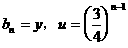 …………10分
…………10分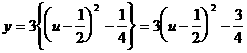
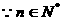 ,
,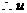 的值分别为
的值分别为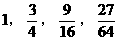 ……,经比较
……,经比较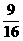 距
距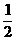 最近…………12分
最近…………12分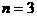 时,
时,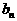 有最小值是
有最小值是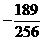 ,
………………………………13分
,
………………………………13分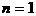 时,
时,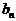 有最大值是0。
…………………………………14分
有最大值是0。
…………………………………14分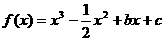
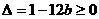
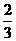 是另一根,f(x)=
是另一根,f(x)=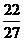 +c
+c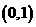 ,如图所示.
,如图所示.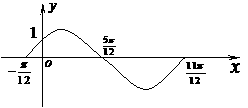 (2)将函数y= f1 (x)的图象按向量a = ( , 0)平移,得到函数 y =
f2 (x),求y=
f1 (x)+ f2 (x)的最大值,并求此时自变量
(2)将函数y= f1 (x)的图象按向量a = ( , 0)平移,得到函数 y =
f2 (x),求y=
f1 (x)+ f2 (x)的最大值,并求此时自变量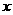 的集合.
的集合.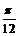 ,得f1(x)=A
sin (2x+j )的图象,
则
,得f1(x)=A
sin (2x+j )的图象,
则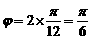 ,∴ f1(x)=A sin (2x+ ), 4分
,∴ f1(x)=A sin (2x+ ), 4分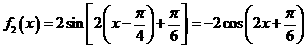 10分
10分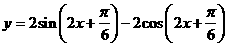
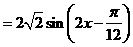 12分
12分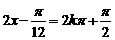 ,即
,即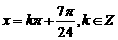 时,
时,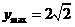
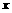 的取值集合为
的取值集合为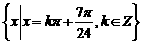 14分
14分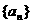 中,首项
中,首项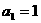 ,数列
,数列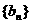 满足
满足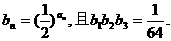
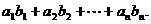
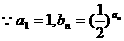 ,
,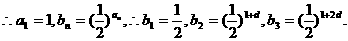
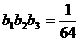 ,解得d=1.
5分
,解得d=1.
5分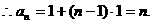 7分
7分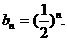
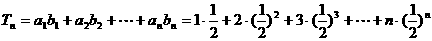 ,
,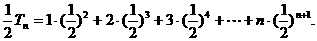 9分
9分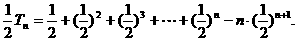 11分
11分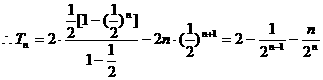 14分
14分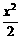 -2x+5.
-2x+5.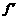 (x)=3x2-x-2=0,得x=1,-
(x)=3x2-x-2=0,得x=1,-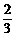 .在(-∞,-
.在(-∞,-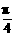 -x)=
-x)=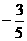 ,
, 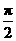 ,求
,求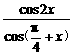 的值.
的值.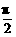 ,
,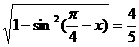 4分
4分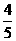 =
=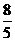 12分
12分