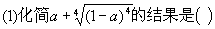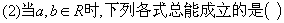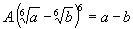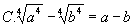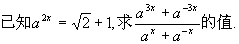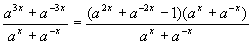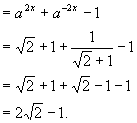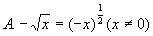0 445863 445871 445877 445881 445887 445889 445893 445899 445901 445907 445913 445917 445919 445923 445929 445931 445937 445941 445943 445947 445949 445953 445955 445957 445958 445959 445961 445962 445963 445965 445967 445971 445973 445977 445979 445983 445989 445991 445997 446001 446003 446007 446013 446019 446021 446027 446031 446033 446039 446043 446049 446057 447348
 、
、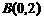 ,C是圆
,C是圆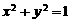 上一个动点,则△ABC的面积的最小值为 .
上一个动点,则△ABC的面积的最小值为 .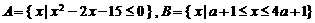 ,
,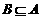 ,则
,则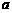 的取值范围是
.
的取值范围是
.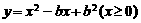 存在反函数的充要条件是
.
存在反函数的充要条件是
.