摘要:圆 圆的定义 点集:{M||OM|=r}.其中定点O为圆心.定长r为半径. 圆的方程 (1)标准方程 圆心在c(a,b).半径为r的圆方程是 (x-a)2+(y-b)2=r2 圆心在坐标原点.半径为r的圆方程是 x2+y2=r2 (2)一般方程 当D2+E2-4F>0时.一元二次方程 x2+y2+Dx+Ey+F=0 叫做圆的一般方程.圆心为(-,-).半径是.配方.将方程x2+y2+Dx+Ey+F=0化为 (x+)2+(y+)2= 当D2+E2-4F=0时.方程表示一个点 (-,-); 当D2+E2-4F<0时.方程不表示任何图形. 点与圆的位置关系 已知圆心C(a,b),半径为r,点M的坐标为(x0,y0).则 |MC|<r点M在圆C内. |MC|=r点M在圆C上. |MC|>r点M在圆C内. 其中|MC|=. (3)直线和圆的位置关系 ①直线和圆有相交.相切.相离三种位置关系 直线与圆相交?有两个公共点 直线与圆相切?有一个公共点 直线与圆相离?没有公共点 ②直线和圆的位置关系的判定 (i)判别式法 到直线Ax+By+C=0的距离d=与半径r的大小关系来判定.
网址:http://m.1010jiajiao.com/timu3_id_4459777[举报]
(2012•河南模拟)两条平行直线和圆的位置关系定义为:若两条平行直线和圆有四个不同的公共点,则称两条平行线和圆“相交”;若两平行直线和圆没有公共点,则称两条平行线和圆“相离”;若两平行直线和圆有一个、两个或三个不同的公共点,则称两条平行线和圆“相切”.已知直线l1:2x-y+a=0,l2:2x-y+a2+1=0和圆:x2+y2+2x-4=0相切,则a的取值范围是( )
 定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的
定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的| 1 |
| 2 |
查看习题详情和答案>>
 如图,在平面斜坐标系XOY中,∠xoy=θ,平面上任意一点P关于斜坐标系的斜坐标这样定义:若
如图,在平面斜坐标系XOY中,∠xoy=θ,平面上任意一点P关于斜坐标系的斜坐标这样定义:若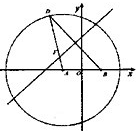 如图,在平面直角坐标系xoy中,圆A:(x+2)2+y2=36,点B(2,0),点D是圆A上的动点,线段BD的垂直平分线交线段AD于点F,设m,n分别为点F,D的横坐标,定义函数m=f(n),给出下列结论:
如图,在平面直角坐标系xoy中,圆A:(x+2)2+y2=36,点B(2,0),点D是圆A上的动点,线段BD的垂直平分线交线段AD于点F,设m,n分别为点F,D的横坐标,定义函数m=f(n),给出下列结论: