3.直线的方程
直线方程的几种形式
|
名称 |
已知条件 |
方程 |
说明 |
|
斜截式 |
斜率k纵截距b |
y=kx+bx |
不包括y轴和平行于y轴的直线 |
|
点斜式 |
点P 1(x1,y1)斜率k |
y-y1=k(x-x1) |
不包括y轴和平行于y轴的直线 |
|
两点式 |
点P1(x1,y1)和P2(x2,y2) |
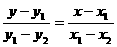 |
不包括坐标轴和平行于坐标轴的直线 |
|
截距式 |
横截距a纵坐标b |
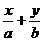 =1 =1 |
不包括坐标轴,平行于坐标轴和过原点的直线 |
|
一般式 |
- |
Ax+By+C=0 |
A、B不同时为0 |
两条直线的位置关系
当直线不平行于坐标轴时:
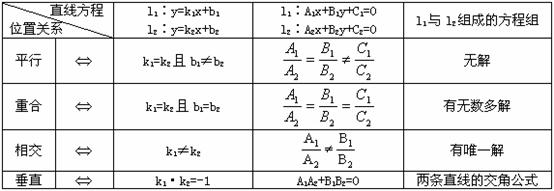
(1)直线l1到l2的角 直线l1依逆时针方向旋转到与l2重合时所转的角,叫做l1 到l2的角.
计算公式
设直线l1,l2的斜率分别是k1,k2,则
tgθ= (k1k2≠-1)
(k1k2≠-1)
(2)两条直线的夹角一条直线到另一条直线的角小于直角的角,即两条直线所成的锐角叫做两条直线所成的角,简称夹角.这时的计算公式为:tgθ=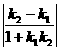
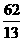 ).求反射光线所在直线方程.
).求反射光线所在直线方程.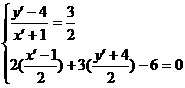 解得
解得 ,再由两点式可得所求直线方程为13x-26y+85=0.
,再由两点式可得所求直线方程为13x-26y+85=0.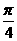 ]和[
]和[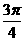 ,π]。
,π]。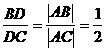 ,从而求得D(
,从而求得D(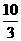 ,
,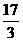 ),故可得│AD│=
),故可得│AD│=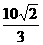 .
.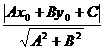
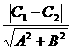 .
.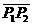 分成两条有向线段
分成两条有向线段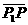 分成两条有向线段
分成两条有向线段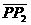 ,则
,则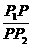
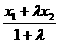 , y=
, y=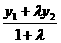 .
.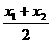 , y=
, y=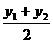 .
.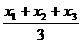 , y=
, y=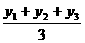
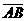 的数量用AB表示.
的数量用AB表示.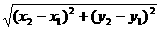
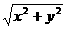 .
.