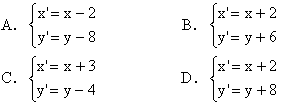摘要:坐标变换 坐标变换 在解析几何中.把坐标系的变换(如改变坐标系原点的位置或坐标轴的方向)叫做 坐标变换.实施坐标变换时.点的位置.曲线的形状.大小.位置都不改变.仅仅只改变点 的坐标与曲线的方程. 坐标轴的平移 坐标轴的方向和长度单位不改变.只改变原点的位置.这种坐标系的变换叫 做坐标轴的平移.简称移轴. 坐标轴的平移公式 设平面内任意一点M.它在原坐标系xOy中的坐标是(x,y).在新坐标系x ′O′y′中的坐标是.设新坐标系的原点O′在原坐标系xOy中的坐标是(h,k).则 (1) 或 (2) 公式叫做平移公式. 中心或顶点在(h,k)的圆锥曲线方程 中心或顶点在(h,k)的圆锥曲线方程见下表. 方 程 焦 点 焦 线 对称轴 椭 圆 x=±+h x=h y=k y=±+k x=h y=k 双曲线 y=±+k x=h y=k y=±+k x=h y=k 抛物线 (y-k)2=2p(x-h) (+h,k) x=-+h y=k (y-k)2=-2p(x-h) (-+h,k) x=+h y=k (x-h)2=2p(y-k) (h, +k) y=-+k x=h (x-h)2=-2p(y-k) (h,- +k) y=+k x=h
网址:http://m.1010jiajiao.com/timu3_id_4459780[举报]
在Excel中产生[0,1]区间上均匀随机数的函数为“rand( )”,在用计算机模拟估计函数y=sinx的图象、直线x=
和x轴在区间[0,
]上部分围成的图形面积时,随机点(a1,b1)与该区域内的点(a,b)的坐标变换公式为( )
| π |
| 2 |
| π |
| 2 |
A、a=a 1+
| ||
| B、a=2(a1-0.5)b=2(b1-0.5) | ||
C、a∈[0,
| ||
D、a=
|