0 445637 445645 445651 445655 445661 445663 445667 445673 445675 445681 445687 445691 445693 445697 445703 445705 445711 445715 445717 445721 445723 445727 445729 445731 445732 445733 445735 445736 445737 445739 445741 445745 445747 445751 445753 445757 445763 445765 445771 445775 445777 445781 445787 445793 445795 445801 445805 445807 445813 445817 445823 445831 447348
 。
。 的底面边长为a,点M在边BC上,△
的底面边长为a,点M在边BC上,△ 是以点M为直角顶点的等腰直角三角形.
是以点M为直角顶点的等腰直角三角形.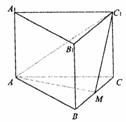
 的大小.
的大小.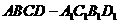 的侧棱
的侧棱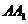 的长是a,底面ABCD是边长AB=2a,BD=a的矩形,E为
的长是a,底面ABCD是边长AB=2a,BD=a的矩形,E为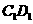 的中点。
的中点。 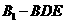 的体积.
的体积.
 正三棱锥P-ABC的底面边长为a,E、F分别是侧棱PB、PC的中点,且E、A、F三点的截面垂直于侧面PBC.
正三棱锥P-ABC的底面边长为a,E、F分别是侧棱PB、PC的中点,且E、A、F三点的截面垂直于侧面PBC. 例2.三棱锥各侧面与底面均成45°角,底面三角形三内角A、B、C满足2B=A+C,最大边与最小边是方程3x2-27x+32=0的两根.
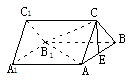
例2.三棱锥各侧面与底面均成45°角,底面三角形三内角A、B、C满足2B=A+C,最大边与最小边是方程3x2-27x+32=0的两根.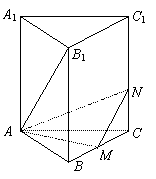 3.如图,正三棱柱ABC-A1B1C1的所有棱长都为4,M是BC的中点,N是CC1上一点,满足MN⊥AB1
3.如图,正三棱柱ABC-A1B1C1的所有棱长都为4,M是BC的中点,N是CC1上一点,满足MN⊥AB1 的体积;
的体积;
 4.如图,三棱柱
4.如图,三棱柱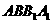 是菱形且垂直于底面,∠
是菱形且垂直于底面,∠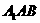 =60°,M是
=60°,M是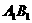 的中点.
的中点.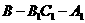 的正切值;
的正切值;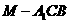 的体积.
的体积.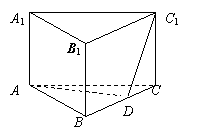 (2)求二面角C-AC1-D的大小.
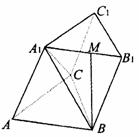
(2)求二面角C-AC1-D的大小.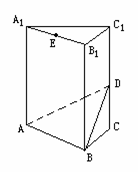 如图,正三棱柱A1B1C1-ABC中,底面边长和侧棱长都是1,D、E分别是C1C和A1B1的中点.
如图,正三棱柱A1B1C1-ABC中,底面边长和侧棱长都是1,D、E分别是C1C和A1B1的中点. 例1、如图,直三棱柱ABC-A1B1C1的底面ABC为等腰直
例1、如图,直三棱柱ABC-A1B1C1的底面ABC为等腰直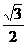 ,D为AB的中点.
,D为AB的中点.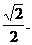 ∴
∴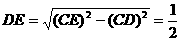 ;
;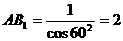 , ∴
, ∴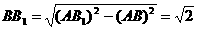 ,
,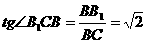 , ∴
, ∴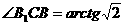 .
.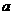
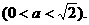
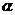 的大小。
的大小。
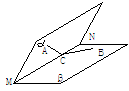
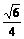 ; (2)arctan
; (2)arctan (提示:求出点A在平面 b 的射影到直线BC的距离为
(提示:求出点A在平面 b 的射影到直线BC的距离为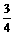 ).
).
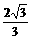 cm;
cm;  .
.
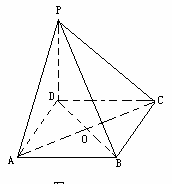 (1)求证:PD⊥平面ABCD;
(1)求证:PD⊥平面ABCD; (1)求证:平面AA1E⊥平面BCD;
(1)求证:平面AA1E⊥平面BCD;