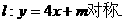8.圆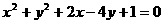 关于直线
关于直线 对称,则ab的取值范
对称,则ab的取值范
围是 ( )
A.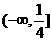 B.
B.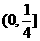 C.
C.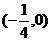 D.
D.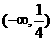
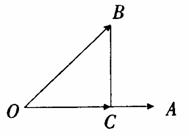 9.如图,非零向量
9.如图,非零向量 ( )
( )
A.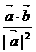 B.
B.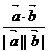
C.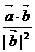 D.
D.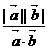
|
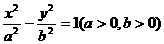 的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是 ( )
的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是 ( )
A.(1,+ ) B.(1,2) C.(1,1+
) B.(1,2) C.(1,1+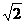 ) D.(2,1+
) D.(2,1+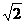 )
)
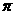 ,②图象关于直线
,②图象关于直线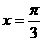 对称;③在
对称;③在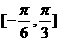 上是增
上是增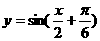 B.
B.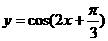
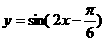 D.
D.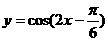
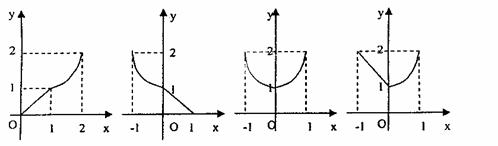 7.已知
7.已知 则下列函数的图象错误的是 ( )
则下列函数的图象错误的是 ( ) 的图象 B.
的图象 B.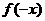 的图象
的图象 的图象 D.
的图象 D.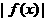 的图象
的图象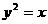 和直线x=1围成图形的面积是 ( )
和直线x=1围成图形的面积是 ( ) 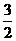 C.
C.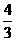 D.
D.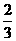
 ,有下列命题
,有下列命题 ;
;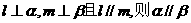 ;
;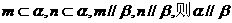 ;
; ;
;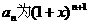 的展开式中含
的展开式中含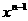 项的系数,则数列
项的系数,则数列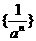 的前n项和为 ( )
的前n项和为 ( )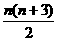 B.
B.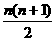 C.
C.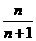 D.
D.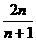
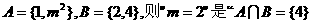 ”的 ( )
”的 ( )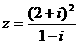 (i是虚数单位)在复平面上对应的点位于 ( )
(i是虚数单位)在复平面上对应的点位于 ( )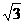 ,BD=CD=1,另一侧面ABC为正三角形。
,BD=CD=1,另一侧面ABC为正三角形。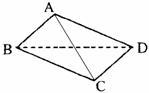 (3)在线段AC上是否存在一点E,使ED与面BCD成30°角。若存在,确定E点的位置,若不存在,请说明理由。
(3)在线段AC上是否存在一点E,使ED与面BCD成30°角。若存在,确定E点的位置,若不存在,请说明理由。 与直线l:
与直线l: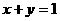 相交于不同的两点A、B
相交于不同的两点A、B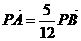 ,求a的值.
,求a的值.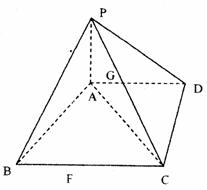 21.(12分)已知四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为直角梯形,∠ADC是直角,AD∥BC,AB⊥AC,G为△PAC的重心,F在线段BC上且CF=2FB
21.(12分)已知四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为直角梯形,∠ADC是直角,AD∥BC,AB⊥AC,G为△PAC的重心,F在线段BC上且CF=2FB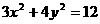 ,试确定m的取值范围,使得椭圆C上有两个不同的点关于直线
,试确定m的取值范围,使得椭圆C上有两个不同的点关于直线