河南省平顶山许昌新乡2008-2009学年高三第三次调研考试
文科数学(必修+选修I)
一、选择题
1.设集合
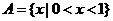 ,
,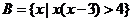
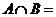
A、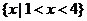 B、
B、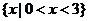 C、
C、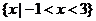 D、
D、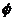
A、160人、140人、100人 B、200人、150人、50人
C、180人、120人、100人 D、250人、100人、50人
2.某校高一、高二、高三的学生人数分别为3200人、2800人、2000人,为了了解学生星期天的睡眠时间,决定抽取400名学生进行抽样调查,则高一、高二、高三应分别抽取
3.已知P、A、B、C是平面内四点,且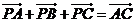 ,那么一定有
,那么一定有
A、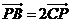 B、
B、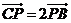 C、
C、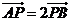 D、
D、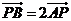
4.已知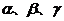 是三个互不重合的平面,
是三个互不重合的平面,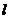 是一条直线,给出下列四个命题
是一条直线,给出下列四个命题
①若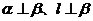 ,则
,则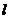 ∥
∥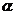 ;
;
②若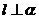 ,
,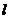 ∥
∥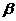 ,则
,则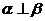
③若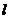 上有两个点到
上有两个点到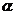 的距离相等,则
的距离相等,则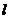 ∥
∥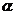 ;
;
④若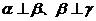 ,则
,则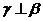 ;
;
其中正确的命题是
A、①③ B、②④ C、①④ D、②③
5.已知奇函数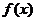 和偶函数
和偶函数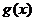 满足
满足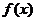 +
+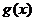 =
=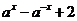 ,若
,若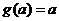 ,则
,则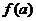
A、1 B、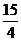 D、
D、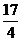
6.在各项都是正数的等比数列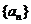 中,首项
中,首项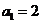 ,前3项和为14,则
,前3项和为14,则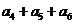 的值为
的值为
A、112 B、114 C、116 D、118
7.关于函数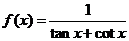 ,下列说法正确的是
,下列说法正确的是
A、最小正周期为π B、图像关于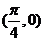 对称
对称
C、函数的最大值为1 D、在区间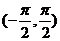 内递增
内递增
8.设正四面体ABCD的四个面的中心分别为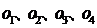 ,则直线
,则直线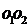 与
与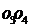 所成角的大小为
所成角的大小为
A 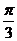 B
B
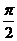 C
C
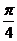 D
D
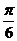
9.函数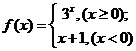 的反函数为
的反函数为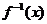 ,则
,则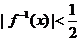 的解集为
的解集为
A、(1,) B、(,1)
C、(,) D、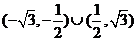
10.双曲线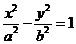 左、右集点分别
左、右集点分别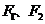 ,过
,过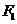 作倾斜角为30°的直线交双曲线右支于M点,若
作倾斜角为30°的直线交双曲线右支于M点,若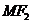 垂直于x轴,则双曲线的离心率为
垂直于x轴,则双曲线的离心率为
A、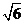 B、
B、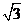 C、
C、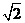 D、
D、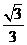
11.从甲、乙等10名同学挑选4名参加某项公益活动,要求甲、乙中至少有1人参加,则不同的挑选方法有
A、70种 B、112种 C、140种 D、168种
12.设P为椭圆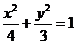 上的任意一点,EF为圆N:
上的任意一点,EF为圆N: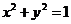 的任一条直径,则
的任一条直径,则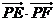 的取值范围是
的取值范围是
A、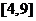 B、
B、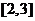 C、
C、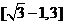 D、
D、
二、填空题
13.在锐角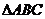 中,角
中,角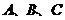 的对边
的对边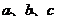 ,且
,且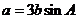 ,则
,则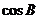 =____
=____
14.若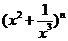 展开式的各项系数和为32,则展开式中的常数项为______
展开式的各项系数和为32,则展开式中的常数项为______
15.若实数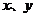 满足
满足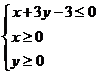 ,则目标函数
,则目标函数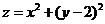 的最大值是_____
的最大值是_____
16.在正方体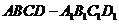 中有如下四个命题
中有如下四个命题
①当P在直线BC1运动时,三棱锥A-D1PC的体积不变
②当P在直线BC1运动时,直线AP与平面ACD1所成角的大小不变;
③当P在直线BC1运动时,二面角P-AD1-C的大小不变;
④当P在直线BC1运动时,直线CP与直线A1B1所成角的大小不变
三解答题
17.在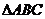 中,已知
中,已知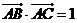 ,
,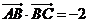
(I)求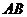 的长度
的长度
(II)若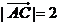 ,求
,求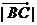
18.设A袋子中装有3个白球,B袋子中装有5个白球3个黄球,它们除颜色外,其余相同。
(I)现从A、B两个袋子中随机地各摸出1个球,求至少有一个黄球的概率;
(II)若从A、B两个袋子中随机地各摸出2个球,求黄球数与白球数相等的概率;
(I)求证: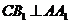 ;
;
(II)求二面角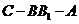 的大小。
的大小。
20.已知正数数列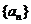 的前
的前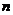 项和
项和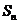 满足
满足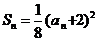 ,
,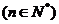
(I)求数列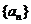 的通项公式
的通项公式
(II)设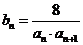 ,
,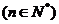 且数列
且数列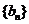 的前
的前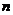 项和为
项和为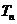 ,如果
,如果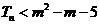 对一切
对一切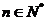 成立,求正数
成立,求正数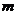 的取值范围。
的取值范围。
21.设 ,
,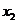 (
(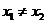 )是函数
)是函数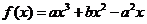
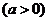 的两个极值点
的两个极值点
(I)若 ,求
,求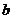 的最大值
的最大值
(II)设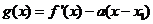 ,
,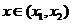 ,当
,当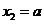 时,求证:
时,求证: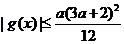
22.设点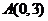 是椭圆
是椭圆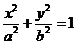 短轴一个端点,
短轴一个端点,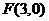 是椭圆的一个焦点,
是椭圆的一个焦点,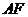 的延长线与椭圆交于点C,直线
的延长线与椭圆交于点C,直线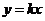 与椭圆相于B、D,与相交于E(E与A、C不重合)
与椭圆相于B、D,与相交于E(E与A、C不重合)
(I)若E是AC的中点,求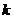 的值
的值
(II)求四边形ABCD面积的最大值。
2008~2009学年新乡许昌平顶山高三第三次调研考试
文科数学答案
一、 DADB CAAB CBCB .
二、13. 14.10 15.13 16.①③④.
14.10 15.13 16.①③④.
17.(本小题满分10分)
解:(Ⅰ)∵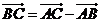 ,∴
,∴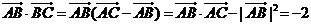 ,
,
∵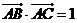 , ∴
, ∴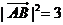 ,
,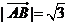 ,即AB边的长度为
,即AB边的长度为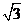 . …5分
. …5分
(Ⅱ)∵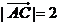 ,∵
,∵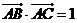 ,∴
,∴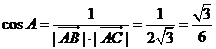 ,
,
由余弦定理得,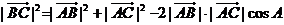 =
=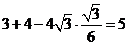 ,
,
∴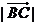 =
=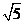 .
………10分
.
………10分
18.(本小题满分12分)
解:(Ⅰ)设M={从A袋中摸出1个黄球},N={从B袋中摸出1个黄球},
则,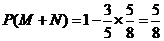 ,即,至少有一个黄球的概率为
,即,至少有一个黄球的概率为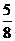 . ………4分
. ………4分
(Ⅱ)从A、B两个袋子中各摸出2个球,黄球与白球数各2个分下列三类:
(?)A中取2黄B中取2白,其概率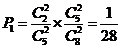 ;
……6分
;
……6分
(?)A中取2白B中取2黄,其概率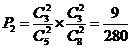 ;
………8分
;
………8分
(?)A中1黄1白B中1黄1白,其概率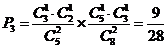 ; …10分
; …10分
∴黄球数与白球数相等的概率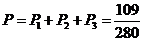 .
……………12分
.
……………12分
19.(本小题满分12分)
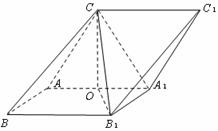
解:(Ⅰ)∵CA=CA1=AB=BB1=1,∴ABB1A1,ABB1A1都是菱形,
∵面积=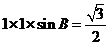 ,又∠ABB1为锐角,∴∠ABB1=60°,
,又∠ABB1为锐角,∴∠ABB1=60°,
∴△ABB1,△AB1A1,△CAA1均为边长为1的等边三角形. ………3分
∵侧面AA1C1C⊥侧面ABB1A1,设O为AA1的中点,则CO⊥平面ABB1A1,
又OB1⊥AA1,∴由三垂线定理可得CB1⊥AA1. ………… 7分
∴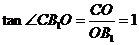 ,
,
∴二面角C-BB1-A的大小为45°. …………12分
20.(本小题满分12分)
解:(I)∵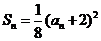 ,∴
,∴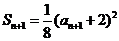 , ……………2分
, ……………2分
两式相减得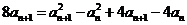 ,∴
,∴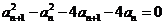 ,
,
∴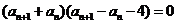 ,又
,又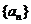 是正数数列,
是正数数列,
∴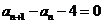 ,∴
,∴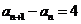 ,∴
,∴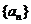 是等差数列.
………4分
是等差数列.
………4分
∵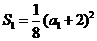 ,∴
,∴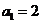 ,∴
,∴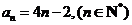 .
……………6分
.
……………6分
(II)∵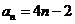 ,∴
,∴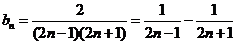 , ……………7分
, ……………7分
∴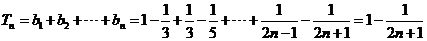 ,……9分
,……9分
∴对一切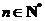 ,必有
,必有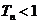 .
……………10分
.
……………10分
故令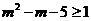 ,∴
,∴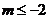 或
或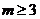 ,
,
又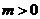 ,∴
,∴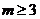 .
………12分
.
………12分
21.(本小题满分12分)
解:(Ⅰ)∵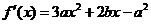 ,∴
,∴ ,
,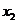 是方程
是方程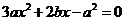 的两根,
的两根,
∴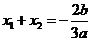 ,
,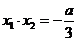 ,
……………2分
,
……………2分
∵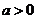 ,∴
,∴ ,
,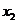 异号,
异号,
由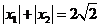 平方得:
平方得: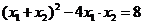 ,
,
∴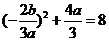 ,∴
,∴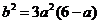 ,显然
,显然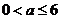 , ……………5分
, ……………5分
令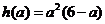 ,则
,则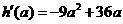 ,由
,由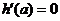 得
得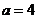 ,
,
∴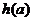 的最大值为
的最大值为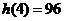 ,即,b的最大值为
,即,b的最大值为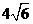 .…………7分
.…………7分
(Ⅱ)由(Ⅰ)知,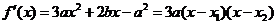 ,
,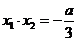 ,
,
当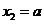 时,
时,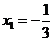 ,∴
,∴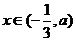 ,这时,
,这时,
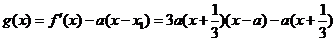
=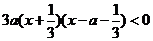 ,
……………10分
,
……………10分
∴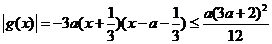 ,当且仅当
,当且仅当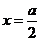 时取等号.…12分
时取等号.…12分
22.(本小题满分12分)
解:(Ⅰ)由题意可知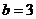 ,
, ,∴
,∴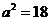 ,即椭圆方程为
,即椭圆方程为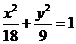 ,
,
∴直线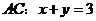 与椭圆的交点
与椭圆的交点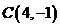 ,
,
∴AC的中点E为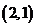 ,∴
,∴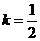 . ……………4分
. ……………4分
(Ⅱ)∵直线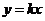 与线段AC:
与线段AC: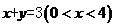 相交,∴
相交,∴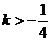 , …………5分
, …………5分
把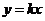 代入椭圆
代入椭圆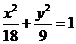 得
得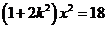 ,∴
,∴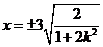 ,
,
∴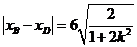 ,∴
,∴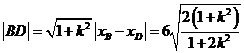 .……………6分
.……………6分
又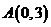 到直线
到直线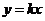 的距离为
的距离为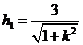 ,
,
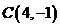 到直线
到直线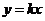 的距离为
的距离为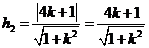 ,…………8分
,…………8分
∴四边形ABCD的面积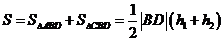
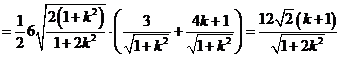 ……………9分
……………9分
∴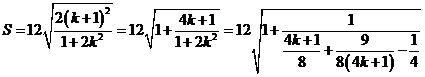
∵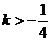 ,∴
,∴ ,当且仅当
,当且仅当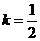 时等号成立,∴
时等号成立,∴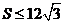 ,
,
∴四边形ABCD的面积的最大值为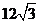 ,此时
,此时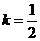 ,即直线正好经过线段AC的中点.……………12分
,即直线正好经过线段AC的中点.……………12分
 21世纪教育网
21世纪教育网
www.1010jiajiao.com
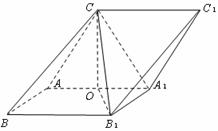
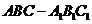 中,侧面
中,侧面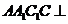 侧面
侧面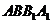 ,侧面
,侧面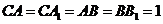 ,
,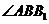 为锐角。
为锐角。