摘要:∵.∴.当且仅当时等号成立.∴.
网址:http://m.1010jiajiao.com/timu_id_299772[举报]
我们将具有下列性质的所有函数组成集合M:函数![]() ,对任意
,对任意![]() 均满足
均满足![]() ,当且仅当
,当且仅当![]() 时等号成立。
时等号成立。
(1)若定义在(0,+∞)上的函数![]() ∈M,试比较
∈M,试比较![]() 与
与![]() 大小.
大小.
(2)设函数g(x)=-x2,求证:g(x)∈M.
查看习题详情和答案>>给出命题:若 是正常数,且
是正常数,且 ,
, ,则
,则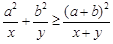 (当且仅当
(当且仅当 时等号成立). 根据上面命题,可以得到函数
时等号成立). 根据上面命题,可以得到函数 (
( )的最小值及取最小值时的x值分别为( )
)的最小值及取最小值时的x值分别为( )
A.11+6 ,
, B.11+6
B.11+6 ,
, C.5,
C.5, D.25,
D.25,
查看习题详情和答案>>
给出命题:若a,b是正常数,且a≠b,x,y∈(0,+∞),则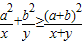 (当且仅当
(当且仅当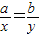 时等号成立).根据上面命题,可以得到函数
时等号成立).根据上面命题,可以得到函数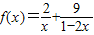 (
(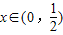 )的最小值及取最小值时的x值分别为( )
)的最小值及取最小值时的x值分别为( )
A.11+6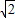 ,
,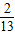
B.11+6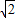 ,
,
C.5,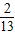
D.25,
查看习题详情和答案>>
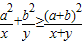 (当且仅当
(当且仅当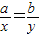 时等号成立).根据上面命题,可以得到函数
时等号成立).根据上面命题,可以得到函数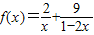 (
(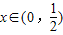 )的最小值及取最小值时的x值分别为( )
)的最小值及取最小值时的x值分别为( )A.11+6
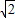 ,
,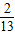
B.11+6
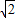 ,
,
C.5,
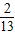
D.25,

查看习题详情和答案>>
已知函数 ,
,
(1)求函数 的定义域;
的定义域;
(2)求函数 在区间
在区间 上的最小值;
上的最小值;
(3)已知 ,命题p:关于x的不等式
,命题p:关于x的不等式 对函数
对函数 的定义域上的任意
的定义域上的任意 恒成立;命题q:指数函数
恒成立;命题q:指数函数 是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
【解析】第一问中,利用由 即
即

第二问中, ,
, 得:
得:

 ,
,

第三问中,由在函数 的定义域上
的任意
的定义域上
的任意 ,
, ,当且仅当
,当且仅当 时等号成立。当命题p为真时,
时等号成立。当命题p为真时, ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以
当命题p为真,命题q为假时;当命题p为假,命题q为真时分为两种情况讨论即可 。
解:(1)由 即
即

(2) ,
, 得:
得:

 ,
,

(3)由在函数 的定义域上
的任意
的定义域上
的任意 ,
, ,当且仅当
,当且仅当 时等号成立。当命题p为真时,
时等号成立。当命题p为真时, ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以
当命题p为真,命题q为假时,
当命题p为假,命题q为真时, ,
,
所以
查看习题详情和答案>>