摘要：∵面积=.又∠ABB1为锐角.∴∠ABB1=60°.∴△ABB1.△AB1A1.△CAA1均为边长为1的等边三角形． ---3分∵侧面AA1C1C⊥侧面ABB1A1.设O为AA1的中点.则CO⊥平面ABB1A1.又OB1⊥AA1.∴由三垂线定理可得CB1⊥AA1． ---- 7分
网址：http://m.1010jiajiao.com/timu_id_299733[举报]
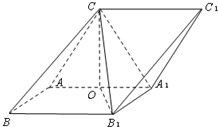如图，在三棱柱ABC-A1B1C1中，侧面AA1CC1⊥侧面ABB1A1，侧面ABB1A1的面积为
| ||
| 2 |
（1）求证：CB1⊥AA1；
（2）求二面角C-BB1-A的大小．
如图，在三棱柱ABC-A1B1C1中，侧面AA1CC1⊥侧面ABB1A1，侧面ABB1A1的面积为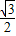
，CA=CA1=AB=BB1=1，∠ABB1为锐角
（1）求证：CB1⊥AA1；
（2）求二面角C-BB1-A的大小．
查看习题详情和答案>>
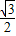，CA=CA1=AB=BB1=1，∠ABB1为锐角（1）求证：CB1⊥AA1；
（2）求二面角C-BB1-A的大小．
查看习题详情和答案>>
已知奇函数f（x）在[-1，0]上单调递减，又α，β为锐角三角形的两内角，则有（ ）
| A、f（sinα-sinβ）≥f（cosα-cosβ） | B、f（sinα-cosβ）＞f（cosα-sinβ） | C、f（sinα-cosβ）≥f（cosα-sinβ） | D、f（sinα-cosβ）＜f（cosα-sinβ） |
已知奇函数f（x）在[-1，0]上为单调减函数，又α，β为锐角三角形内角，则（ ）
| A、f（cosα）＞f（cosβ） | B、f（sinα）＞f（sinβ） | C、f（sinα）＜f（cosβ） | D、f（sinα）＞f（cosβ） |