摘要:解:(I)∵.∴. -----2分
网址:http://m.1010jiajiao.com/timu_id_299737[举报]
已知△ABC的内角 满足
满足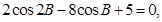 若
若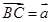 ,
,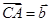 且
且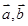 满足:
满足: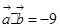 ,
,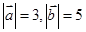 ,
,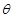 为
为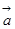 与
与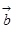 的夹角.
的夹角.
(Ⅰ)求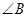 ;
;
(Ⅱ)求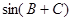 ;
;
【解析】第一问利用二倍角公式化简∵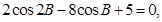 ∴
∴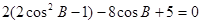 ∴
∴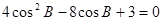 ∴
∴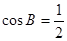 或
或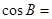
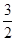 (舍去)又角B是△ABC的内角∴
(舍去)又角B是△ABC的内角∴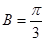
第二问中∵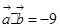 ,
,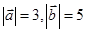 ,
,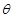 为
为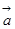 与
与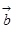 的夹角
的夹角
∴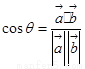 =
=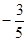 又
又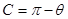 ∴
∴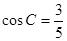 ,
,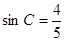 ∴
∴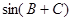 =
=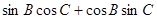 =
=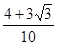
(Ⅰ) 解:∵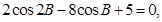 ∴
∴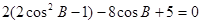
∴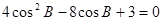 ∴
∴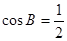 或
或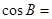
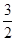 (舍去)…………2分
(舍去)…………2分
又角B是△ABC的内角∴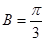 ………………2分
………………2分
(Ⅱ) 解:∵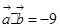 ,
,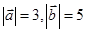 ,
,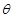 为
为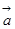 与
与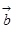 的夹角
的夹角
∴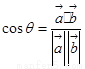 =
=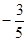 ………………2分
………………2分
又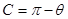 ∴
∴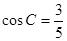 ,
,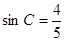 ………………2分
………………2分
∴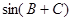 =
=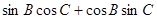 =
=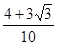
查看习题详情和答案>>
已知 S=1+(1+3)+(1+3+5)+(1+3+5+7)+…+(1+3+5+…+199)
(Ⅰ)下面给出求S的算法,请将空白部分补充完整;
(Ⅱ)请将求S的流程图补充完整,内容直接填在程序框图中;
解:(Ⅰ)算法分析:(1)S=0,T=0,i=1;
(2)将T+2i-1赋值给T,将S+T赋值给S;
(3)将 赋值给i;
(4) ;
(5)输出S,结束运算.
(Ⅱ)流程图:

查看习题详情和答案>>
(Ⅰ)下面给出求S的算法,请将空白部分补充完整;
(Ⅱ)请将求S的流程图补充完整,内容直接填在程序框图中;
解:(Ⅰ)算法分析:(1)S=0,T=0,i=1;
(2)将T+2i-1赋值给T,将S+T赋值给S;
(3)将
(4)
(5)输出S,结束运算.
(Ⅱ)流程图:

(2012•三明模拟)(1)选修4-2:矩阵与变换
设矩阵M=
.
(I)若a=2,b=3,求矩阵M的逆矩阵M-1;
(II)若曲线C:x2+4xy+2y2=1在矩阵M的作用下变换成曲线C':x2-2y2=1,求a+b的值.
(2)选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中x轴的正半轴重合.圆C的参数方程为
(α为参数),点Q极坐标为(2,
).
(Ⅰ)化圆C的参数方程为极坐标方程;
(Ⅱ)若点P是圆C上的任意一点,求P、Q两点距离的最小值.
(3)选修4-5:不等式选讲
设函数f(x)=|x+1|+|x-2|.
(Ⅰ)求y=f(x)的最小值;
(Ⅱ)若关于x的不等式f(x)≥4的解集为A,求集合A.
查看习题详情和答案>>
设矩阵M=
|
(I)若a=2,b=3,求矩阵M的逆矩阵M-1;
(II)若曲线C:x2+4xy+2y2=1在矩阵M的作用下变换成曲线C':x2-2y2=1,求a+b的值.
(2)选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中x轴的正半轴重合.圆C的参数方程为
|
| 7π |
| 4 |
(Ⅰ)化圆C的参数方程为极坐标方程;
(Ⅱ)若点P是圆C上的任意一点,求P、Q两点距离的最小值.
(3)选修4-5:不等式选讲
设函数f(x)=|x+1|+|x-2|.
(Ⅰ)求y=f(x)的最小值;
(Ⅱ)若关于x的不等式f(x)≥4的解集为A,求集合A.