摘要:∴.∴.显然. -----5分
网址:http://m.1010jiajiao.com/timu_id_299752[举报]
已知函数 , 其中
, 其中 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,求曲线
时,求曲线 的单调区间与极值.
的单调区间与极值.
【解析】第一问中利用当 时,
时, ,
,
 ,得到切线方程
,得到切线方程
第二问中,

对a分情况讨论,确定单调性和极值问题。
解: (1) 当 时,
时, ,
,
 ………………………….2分
………………………….2分

 切线方程为:
切线方程为:  …………………………..5分
…………………………..5分
(2) 
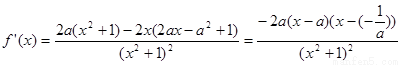 …….7
…….7 分
分
分类: 当 时, 很显然
时, 很显然
 的单调增区间为:
的单调增区间为:  单调减区间:
单调减区间:  ,
,
 ,
,  ………… 11分
………… 11分
当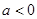 时
时 的单调减区间:
的单调减区间:  单调增区间:
单调增区间: 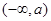 ,
,

 ,
, 
查看习题详情和答案>>
(1)已知 ,且
,且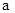 为第三象限角,求
为第三象限角,求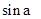 的值
的值
(2)已知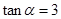 ,计算
,计算 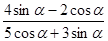 的值 (本小题满分10分)
的值 (本小题满分10分)
【解析】第一问利用∵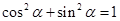 ,
,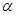 为第三象限角
为第三象限角
∴ 
(2)中显然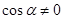
∴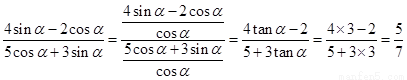
解:(1)∵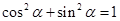 ,
,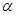 为第三象限角
为第三象限角
∴  ………………5分
………………5分
(2)显然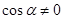
∴ 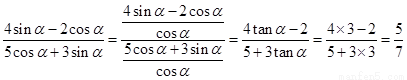
查看习题详情和答案>>
(2011•扬州三模)某次考试共有8道选择题,每道选择题有4个选项,其中只有一个是正确的;评分标准为:“每题只有一个选项是正确的,选对得5分,不选或选错得0分.”某考生每道题都给出一个答案,已确定有5道题的答案是正确的,而其余3道题中,有一道题可判断出两个选项是错误的,有一道题可以判断出一个选项是错误的,还有一道题因不了解题意而乱猜,试求该考生:
(Ⅰ)得40分的概率;
(Ⅱ)所得分数ξ的数学期望.
查看习题详情和答案>>
(Ⅰ)得40分的概率;
(Ⅱ)所得分数ξ的数学期望.
选做题:请考生在下列两题中任选一题作答.若两题都做,则按做的第一题评阅计分.本题共5分.
(1)(不等式选讲)若实数x、y满足|x|+|y|≤1,则x2-xy+y2的最大值为
(2)(坐标系与参数方程)若直线
(t为参数)与直线4x+ky=1垂直,则常数k=
查看习题详情和答案>>
(1)(不等式选讲)若实数x、y满足|x|+|y|≤1,则x2-xy+y2的最大值为
1
1
.(2)(坐标系与参数方程)若直线
|
-6
-6
.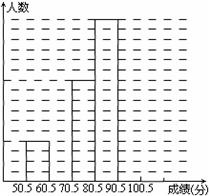 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 |
(Ⅱ)补全频数直方图;
(Ⅲ)学校决定成绩在75.5~85.5分的学生为二等奖,问该校获得二等奖的学生约为多少人? 查看习题详情和答案>>