安徽省马鞍山市2009届高中毕业班第一次教学质量检测
高三数学试题
考生注意事项:
1. 答题前,务必在试题卷、答题卡规定的地方填写自己的座位号、姓名,并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致.
2. 答第Ⅰ卷时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.
3. 答第Ⅱ卷时,必须用
4. 考试结束,监考员将试题卷和答题卡一并收回.
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B)

如果事件A、B相互独立,那么 其中R表示球的半径
P(A?B)=P(A)?P(B)
如果事件A在一次试验中发生的概率是 球的体积公式
P,那么n次独立重复试验中恰好发生k

次的概率 其中R表示球的半径
其中R表示球的半径
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合要求的,请在答题卡上将正确选项的代号涂黑.
(1)满足 ,且
,且 的集合
的集合 的个数是( )
的个数是( )
A.1 B.
(2)设z1 = 1 ? 2i , z2 = 1+ i , 则复数z =  在复平面内对应的点位于
在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(3)给出命题:若函数 是幂函数,则函数
是幂函数,则函数 的图象不过第四象限.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( )
的图象不过第四象限.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( )
A.3 B.2 C.1 D.0
 (4)右图是根据《安徽统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为( )
(4)右图是根据《安徽统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为( )
A.304.6 B.303.6
C.302.6 D.301.6
(5) 展开式中的常数项为( )
展开式中的常数项为( )
A. B.1320 C.
B.1320 C. D.220
D.220
(6)设 ,则不等式
,则不等式 的解集为
的解集为
A.  B.
B. C.
C.  D.
D.
(7)已知{ }是等差数列,
}是等差数列, ,
, ,则过点
,则过点 ,
,
|
 C.
C. D.
D.
 是直线
是直线 垂直的( )
垂直的( ) 平面
平面 ,
, ,点
,点 ,
, ,直线
,直线 ,直线
,直线 ,直线
,直线 ,则下列四种位置关系中,不一定成立的是( )
,则下列四种位置关系中,不一定成立的是( ) B.
B. C.
C. D.
D.
 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时,
时,  ,如果关于
,如果关于 的方程
的方程 有解,记所有解的和为
有解,记所有解的和为 ,则
,则 B.
B. C.
C. D.
D.
 成立的
成立的 B.
B.  C.
C.  D.
D.
 的取值范围是
的取值范围是 A.(
A.( ) B.
) B. ∪
∪
 D.
D.
 (13)如图是一个几何体的三视图,则这个几何体的表面积和体积分别为 ;
(13)如图是一个几何体的三视图,则这个几何体的表面积和体积分别为 ; ,则输出的
,则输出的 ;
; 时,函数
时,函数 的最小值为 ;
的最小值为 ; 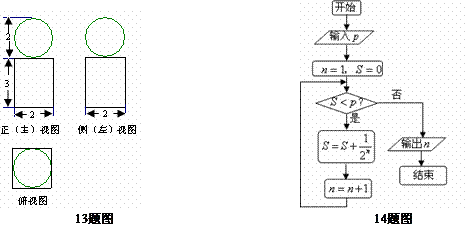
 满足
满足 ,则
,则 的夹角为
的夹角为 ;
; ?
? >0”是“
>0”是“ 的图象按向量
的图象按向量 ;
; 中,若
中,若
 ,则
,则 (
( ,
, )为偶函数,且函数
)为偶函数,且函数 .(
.( 的值;
的值; 个单位后,得到函数
个单位后,得到函数 的图象,求
的图象,求 的单调递减区间.
的单调递减区间. ;如果投资乙项目,一年后可能获利20%,也可能损失20%,这两种情况发生的概率分别为
;如果投资乙项目,一年后可能获利20%,也可能损失20%,这两种情况发生的概率分别为 和
和 ).
).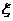 表示投资收益(收益=回收资金-投资资金),求
表示投资收益(收益=回收资金-投资资金),求 ;
; 的取值范围.
的取值范围.

 .
. 时, 求证
时, 求证 在
在 内是减函数;
内是减函数; 在
在 中,
中, ,
, ,
, .
. 是等比数列;
是等比数列; 项和
项和 ;
; ,对任意
,对任意 (22)(本小题满分13分)已知椭圆
(22)(本小题满分13分)已知椭圆 的长轴长为4,A,B,C是椭圆上的三点,点A是长轴的一个顶点,BC过椭圆的中心O,且
的长轴长为4,A,B,C是椭圆上的三点,点A是长轴的一个顶点,BC过椭圆的中心O,且 ,
, ,如图.
,如图. 的平分线垂直于OA,是否总存在实数
的平分线垂直于OA,是否总存在实数 ,使得
,使得 ?请说明理由.
?请说明理由. ; (14) 4; (15)3 ; 16)①③④.
; (14) 4; (15)3 ; 16)①③④.
 .………………………………………………………………………2分
.………………………………………………………………………2分  ,
, 恒成立,
恒成立, .
. ,
, .因为
.因为 .
. .所以
.所以 …………5分.
…………5分. ,所以
,所以 .故
.故 . …………………………6分
. …………………………6分 . ……………………………………………………………7分
. ……………………………………………………………7分 的图象,
的图象, .……………………9分
.……………………9分 (
( ),……10分
),……10分 (
( (
(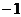 . ……………………2分
. ……………………2分
 .…………………………………………………………………6分
.…………………………………………………………………6分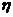 表示10万元投资乙项目的收益,则
表示10万元投资乙项目的收益,则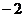
 . ………………………10分
. ………………………10分  ≥
≥ ≤
≤ .??????????????????????? 4分
.??????????????????????? 4分 表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”.
表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”. ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, .共15个基本结果.
.共15个基本结果. .………………………………………………………………12分
.………………………………………………………………12分 又、,∴
又、,∴ 平面BDE且AM
平面BDE且AM 平面BDE,∴AM∥平面BDE. ………4分
平面BDE,∴AM∥平面BDE. ………4分 =,∴的夹角为60°…8分
=,∴的夹角为60°…8分 平面BDE,故HN⊥AC ………………………………………………………………6分
平面BDE,故HN⊥AC ………………………………………………………………6分 (Ⅱ) EH=HD时,H为DE的中点,取CD中点S,
(Ⅱ) EH=HD时,H为DE的中点,取CD中点S,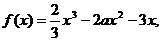
 ……………………………………………………………1分
……………………………………………………………1分 …………………………………………………………3分
…………………………………………………………3分 的图象开口向上,
的图象开口向上, , ………………………………………………………………………5分
, ………………………………………………………………………5分 …8分
…8分 ,则
,则 ………………………………9分
………………………………9分 时, ∵
时, ∵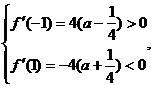
 内
内 在
在 内
内
 时, 同理可知,
时, 同理可知,  …………………………………………12分
…………………………………………12分 ,
, ,所以数列
,所以数列 ,且公比为
,且公比为 的等比数列.………………4分
的等比数列.………………4分 ,于是数列
,于是数列 . ………6分
. ………6分 所以数列
所以数列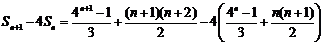
 .
. ,
, ,
, …………………………………………………………………………2分
…………………………………………………………………………2分  ,
, ,即
,即 为等腰直角三角形,……………………………4分
为等腰直角三角形,……………………………4分 ,代入椭圆方程得:
,代入椭圆方程得: ,
, ;………………………………………………………………6分
;………………………………………………………………6分 ,……………………………7分
,……………………………7分 ,则
,则 ,………………………………………8分
,………………………………………8分 ,则CQ:
,则CQ: ,
, ,………………9分
,………………9分 是方程
是方程 的一个根,
的一个根, ,以
,以 代k得
代k得 ,…10分
,…10分 ,故
,故