摘要:① 非零向量满足.则的夹角为,
网址:http://m.1010jiajiao.com/timu_id_295673[举报]
给出下列4个命题:
![]() ① 非零向量
① 非零向量![]() 满足
满足![]() ,则
,则![]() 的夹角为
的夹角为![]() ;
;
![]() ②“
②“ ![]() ?
?![]() >0”是“
>0”是“![]() 的夹角为锐角”的充要条件;
的夹角为锐角”的充要条件;
![]() ③ 将函数
③ 将函数![]() 的图象按向量
的图象按向量![]() =(-1,0)平移,得到的图象对应的函数表达式为
=(-1,0)平移,得到的图象对应的函数表达式为![]() ;
;
![]() ④在
④在![]() 中,若
中,若![]()
![]() ,则
,则![]() 为等腰三角形.
为等腰三角形.
一非零向量列{an}满足a1=(x1,y1),an=(xn,yn)=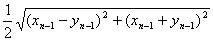 (xn-1-yn-1,xn-1+yn-1)(n≥2),
(xn-1-yn-1,xn-1+yn-1)(n≥2),
(1)证明:{|an|}是等比数列;
(2)求an-1与an的夹角θn(n≥2),若bn=2nθn-1,Sn=b1+b2+…+bn,求Sn;
(3)设a1=(1,2),把a1,a2,…,an,…中所有与a1共线的向量按照原来的顺序排成一列,记为b1,b2,…,bn,…,令![]() =b1+b2+b3+…+bn(O为坐标原点),
=b1+b2+b3+…+bn(O为坐标原点),
求点列{Bn}的极限点B的坐标(注:若点Bn的坐标为(tn,sn)且![]() tn=t,
tn=t,![]() sn=s,则点B(t,s)为点列{Bn}的极限点).
sn=s,则点B(t,s)为点列{Bn}的极限点).
一非零向量列{an}满足:a1=(x1,y1),an=(xn,yn)= (xn-1-yn-1,xn-1+yn-1)(n≥2),
(xn-1-yn-1,xn-1+yn-1)(n≥2),
(1)证明:{|an|}是等比数列;
(2)求an-1与an的夹角θn(n≥2),若bn=2nθn-1,Sn=b1+b2+…bn,求Sn;
(3)设a1=(1,2),把a1,a2,…,an,…中所有与a1共线的向量按照原来的顺序排成一列,记为b1,b2,…,bn,…,令Obn=b1+b2+b3+…+bn(O为坐标原点),求点列{Bn}的极限点B的坐标(注:若点Bn的坐标为(tn,sn)且![]() tn=t,
tn=t,![]() sn=s,则点B(t,s)为点列{Bn}的极限点).
sn=s,则点B(t,s)为点列{Bn}的极限点).
 满足
满足

 。给出以下结论:
。给出以下结论: 是等差数列,2。
是等差数列,2。 ;3。设
;3。设 ,则数列
,则数列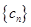 的前n项和为
的前n项和为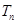 ,当且仅当n=2时,
,当且仅当n=2时, 与
与 的夹角为
的夹角为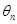 (
( ),均有
),均有 。其中所有正确结论的序号是____
。其中所有正确结论的序号是____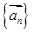 满足
满足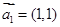 ,
,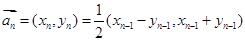
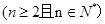 。给出以下结论:
。给出以下结论: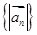 是等差数列,2。
是等差数列,2。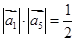 ;3。设
;3。设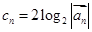 ,则数列
,则数列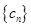 的前n项和为
的前n项和为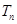 ,当且仅当n=2时,
,当且仅当n=2时,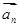 与
与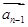 的夹角为
的夹角为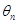 (
(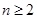 ),均有
),均有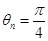 。其中所有正确结论的序号是____
。其中所有正确结论的序号是____