网址:http://m.1010jiajiao.com/timu_id_295740[举报]
如图,三棱锥 中,侧面
中,侧面 底面
底面 ,
,  ,且
,且 ,
, .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面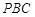 ;
;
(Ⅱ)若 为侧棱PB的中点,求直线AE与底面
为侧棱PB的中点,求直线AE与底面 所成角的正弦值.
所成角的正弦值.

【解析】第一问中,利用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以 第二问中结合取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,因为PA=PC,所以PO⊥AC,同(Ⅰ)易证
第二问中结合取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,因为PA=PC,所以PO⊥AC,同(Ⅰ)易证 平面ABC,又EH//PO,所以EH平面
平面ABC,又EH//PO,所以EH平面 ABC ,
ABC ,
则 为直线AE与底面ABC 所成角,
为直线AE与底面ABC 所成角,

解
(Ⅰ) 证明:由用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以
………………………………………………6分
(Ⅱ)如图, 取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,
因为PA=PC,所以PO⊥AC,同(Ⅰ)易证 平面ABC,
平面ABC,
又EH//PO,所以EH平面 ABC ,
ABC ,
则 为直线AE与底面ABC 所成角,
为直线AE与底面ABC 所成角,
且 ………………………………………10分
………………………………………10分
又PO=1/2AC= ,也所以有EH=1/2PO=
,也所以有EH=1/2PO= ,
,
由(Ⅰ)已证 平面PBC,所以
平面PBC,所以 ,即
,即 ,
,
故 ,
,
于是
所以直线AE与底面ABC 所成角的正弦值为

查看习题详情和答案>>
如图,在直三棱柱 中,底面
中,底面 为等腰直角三角形,
为等腰直角三角形, ,
, 为棱
为棱 上一点,且平面
上一点,且平面 平面
平面 .
.
(Ⅰ)求证: 点为棱
点为棱 的中点;
的中点;
(Ⅱ)判断四棱锥 和
和 的体积是否相等,并证明。
的体积是否相等,并证明。

【解析】本试题主要考查了立体几何中的体积问题的运用。第一问中,
易知 ,
, 面
面 。由此知:
。由此知: 从而有
从而有 又点
又点 是
是 的中点,所以
的中点,所以 ,所以
,所以 点为棱
点为棱 的中点.
的中点.
(2)中由A1B1⊥平面B1C1CD,BC⊥平面A1ABD,D为BB1中点,可以得证。
(1)过点 作
作 于
于 点,取
点,取 的中点
的中点 ,连
,连 。
。 面
面 面
面 且相交于
且相交于 ,面
,面 内的直线
内的直线 ,
, 面
面 。……3分
。……3分
又 面
面 面
面 且相交于
且相交于 ,且
,且 为等腰三角形,易知
为等腰三角形,易知 ,
, 面
面 。由此知:
。由此知: ,从而有
,从而有 共面,又易知
共面,又易知 面
面 ,故有
,故有 从而有
从而有 又点
又点 是
是 的中点,所以
的中点,所以 ,所以
,所以 点为棱
点为棱 的中点.
…6分
的中点.
…6分
(2)相等.ABC-A1B1C1为直三棱柱,∴BB1⊥A1B1,BB1⊥BC,又A1B1⊥B1C1,BC⊥AB,
∴A1B1⊥平面B1C1CD,BC⊥平面A1ABD(9分)∴VA1-B1C1CD=1 /3 SB1C1CD•A1B1=1/ 3 ×1 2 (B1D+CC1)×B1C1×A1B1VC-A1ABD=1 /3 SA1ABD•BC=1 /3 ×1 2 (BD+AA1)×AB×BC∵D为BB1中点,∴VA1-B1C1CD=VC-A1ABD
查看习题详情和答案>>
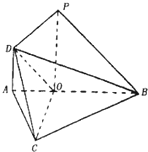 如图,在△ABC中,已知∠ABC=45°,O在AB上,且OB=OC=
如图,在△ABC中,已知∠ABC=45°,O在AB上,且OB=OC=| 2 |
| 3 |
| 1 |
| 2 |
(I)求证:PB∥平面COD;
(II)求证:PD⊥平面COD. 查看习题详情和答案>>
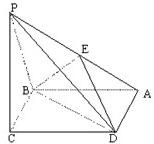 已知四棱锥P-ABCD的底面是边长为a的菱形,∠ABC=120°,又PC⊥平面ABCD,PC=a,E是PA的中点.
已知四棱锥P-ABCD的底面是边长为a的菱形,∠ABC=120°,又PC⊥平面ABCD,PC=a,E是PA的中点.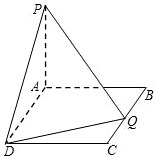 如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.
如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.