摘要:由得是方程的一个根.
网址:http://m.1010jiajiao.com/timu_id_295772[举报]
我市某高中的一个综合实践研究小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差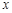 (°C) (°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 (个) (个) | 22 | 25 | 29 | 26 | 16 | 12 |
该综合实践研究小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出
 关于
关于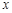 的线性回归方程
的线性回归方程 .
.(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
参考数据:
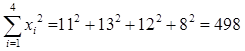 ;
;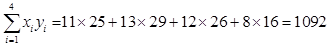 .
查看习题详情和答案>>
.
查看习题详情和答案>>
我市某高中的一个综合实践研究小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
该综合实践研究小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出 关于
关于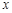 的线性回归方程
的线性回归方程 .
.
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
参考数据: ;
;
 .
.
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差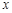 (°C) (°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 (个) (个) | 22 | 25 | 29 | 26 | 16 | 12 |
该综合实践研究小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出
 关于
关于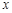 的线性回归方程
的线性回归方程 .
.(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
参考数据:
 ;
; .
.已知![]() ,且方程f(x)+4x-8=0有两个不同的正根,其中一根是另一根的3倍,记等差数列{an}、{bn}的前项和分别为Sn,Tn且
,且方程f(x)+4x-8=0有两个不同的正根,其中一根是另一根的3倍,记等差数列{an}、{bn}的前项和分别为Sn,Tn且![]() (n∈N+).
(n∈N+).

(1)若![]() ,求g(n)的最大值;
,求g(n)的最大值;
(2)若![]() ,数列{bn}的公差为3,试问在数列{an}与{bn}中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列{cn}的通项公式;若不存在,请说明理由.
,数列{bn}的公差为3,试问在数列{an}与{bn}中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列{cn}的通项公式;若不存在,请说明理由.
(3)若![]() ,数列{bn}的公差为3,且
,数列{bn}的公差为3,且![]() ,
,![]() .试证明:
.试证明:![]() .
.
已知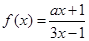 ,且方程
,且方程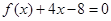 有两个不同的正根,其中一根是另一根的
有两个不同的正根,其中一根是另一根的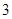 倍,记等差数列
倍,记等差数列 、
、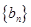 的前
的前 项和分别为
项和分别为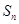 ,
, 且
且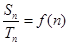 (
(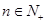 )。
)。
(1)若 ,求
,求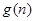 的最大值;
的最大值;
(2)若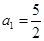 ,数列
,数列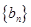 的公差为3,试问在数列
的公差为3,试问在数列 与
与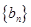 中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列
中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列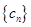 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
(3)若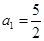 ,数列
,数列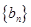 的公差为3,且
的公差为3,且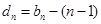 ,
,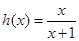 .
.
试证明: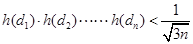 .
.
查看习题详情和答案>>
下表是我国一个工业城市每年中度以上污染的天数,由于以前只注重经济发展,没有过多的考虑工业发展对环境的影响,近几年来,该市加大了对污染企业的治理整顿,环境不断得到改善。
|
年份(x) |
2005年 |
2006年 |
2007年 |
2008年 |
2009年 |
|
中度以上污染的天数(y) |
90 |
74 |
62 |
54 |
45 |
(1)请根据上表提供的数据,用最小二乘法求出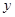 关于
关于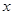 的线性回归方程
的线性回归方程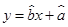 ;
;
(2)按照环境改善的趋势,估计2012年中度以上污染的天数。
(3)在以上5年中任取2年,至少有1年中度以上污染的天数小于60天的概率有多大。
(可用公式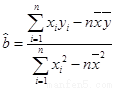 ,
, 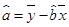 )
)
查看习题详情和答案>>