摘要:17.解:(Ⅰ)
网址:http://m.1010jiajiao.com/timu_id_295698[举报]
解:(Ⅰ)设![]() :
:![]()
![]() ,其半焦距为
,其半焦距为![]()
![]() .则
.则![]() :
:![]() .
.
由条件知![]() ,得
,得![]() .
.
![]() 的右准线方程为
的右准线方程为![]() ,即
,即![]() .
.
![]() 的准线方程为
的准线方程为![]() .
.
由条件知![]() , 所以
, 所以![]() ,故
,故![]() ,
,![]() .
.
从而![]() :
:![]() ,
, ![]() :
:![]() .
.
(Ⅱ)由题设知![]() :
:![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() .
.
由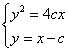 ,得
,得![]() ,所以
,所以![]() .
.
而![]() ,由条件
,由条件![]() ,得
,得![]() .
.
由(Ⅰ)得![]() ,
,![]() .从而,
.从而,![]() :
:![]() ,即
,即![]() .
.
由 ,得
,得![]() .所以
.所以![]() ,
,![]() .
.
故![]() .
.
(Ⅰ)解关于x的不等式:x2-2x+1-a2≥0;
(Ⅱ)已知集合A是函数y=lg(20+8x-x2)的定义域,p:x∈A,q:x2-2x+1-a2≥0(a>0),若?p是q的充分不必要条件,求a的取值范围.
查看习题详情和答案>>
(Ⅱ)已知集合A是函数y=lg(20+8x-x2)的定义域,p:x∈A,q:x2-2x+1-a2≥0(a>0),若?p是q的充分不必要条件,求a的取值范围.
(Ⅰ)阅读理解:
①对于任意正实数a,b,∵(
-
)2≥0, ∴a-2
+b≥0,∴a+b≥2
只有当a=b时,等号成立.
②结论:在a+b≥2
(a,b均为正实数)中,若ab为定值p,则a+b≥2
,
只有当a=b时,a+b有最小值2
.
(Ⅱ)结论运用:根据上述内容,回答下列问题:(提示:在答题卡上作答)
①若m>0,只有当m= 时,m+
有最小值 .
②若m>1,只有当m= 时,2m+
有最小值 .
(Ⅲ)探索应用:
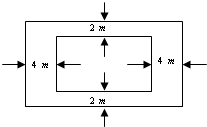
学校要建一个面积为392m2的长方形游泳池,并且在四周要修建出宽为2m和4m的小路(如图).问游泳池的长和宽分别为多少米时,共占地面积最小?并求出占地面积的最小值.
查看习题详情和答案>>
①对于任意正实数a,b,∵(
| a |
| b |
| ab |
| ab |
只有当a=b时,等号成立.
②结论:在a+b≥2
| ab |
| p |
只有当a=b时,a+b有最小值2
| p |
(Ⅱ)结论运用:根据上述内容,回答下列问题:(提示:在答题卡上作答)
①若m>0,只有当m=
| 1 |
| m |
②若m>1,只有当m=
| 8 |
| m-1 |
(Ⅲ)探索应用:
学校要建一个面积为392m2的长方形游泳池,并且在四周要修建出宽为2m和4m的小路(如图).问游泳池的长和宽分别为多少米时,共占地面积最小?并求出占地面积的最小值.
