摘要:即在内是增函数, 在内是减函数.
网址:http://m.1010jiajiao.com/timu_id_295751[举报]
已知函数 ,(
,(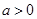 ),
),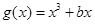
(1)若曲线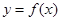 与曲线
与曲线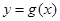 在它们的交点(1,c)处具有公共切线,求a,b的值
在它们的交点(1,c)处具有公共切线,求a,b的值
(2)当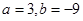 时,若函数
时,若函数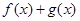 在区间[k,2]上的最大值为28,求k的取值范围
在区间[k,2]上的最大值为28,求k的取值范围
【解析】(1)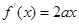 ,
,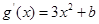
∵曲线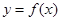 与曲线
与曲线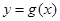 在它们的交点(1,c)处具有公共切线
在它们的交点(1,c)处具有公共切线
∴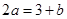 ,
,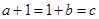
∴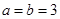
(2)当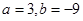 时,
时,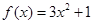 ,
,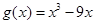 ,
,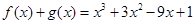
令 ,则
,则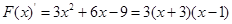 ,令
,令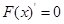 ,
, ∴
∴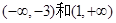 为单调递增区间,
为单调递增区间,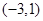 为单调递减区间,其中F(-3)=28为极大值,所以如果区间[k,2]最大值为28,即区间包含极大值点
为单调递减区间,其中F(-3)=28为极大值,所以如果区间[k,2]最大值为28,即区间包含极大值点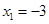 ,所以
,所以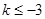
【考点定位】此题应该说是导数题目中较为常规的类型题目,考查的切线,单调性,极值以及最值问题都是课本中要求的重点内容,也是学生掌握比较好的知识点,在题目中能够发现F(-3)=28,和分析出区间[k,2]包含极大值点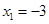 ,比较重要
,比较重要
查看习题详情和答案>>
根据定义讨论(或证明)函数增减性的一般步骤是:
(1)设x1、x2是给定区间内的任意两个值且x1<x2;
(2)作差f(x1)-f(x2),并将此差化简、变形;
(3)判断f(x1)-f(x2)的正负,从而证得函数的增减性.
利用函数的单调性可以把函数值的大小比较的问题转化为自变量的大小比较的问题.
函数的单调性只能在函数的定义域内来讨论.这即是说,函数的单调区间是其定义域的________.
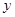 与档次
与档次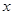 之间的函数关系式,并写出
之间的函数关系式,并写出