网址:http://m.1010jiajiao.com/timu_id_3980664[举报]
( (本小题满分13分)
随着国家政策对节能环保型小排量车的调整,两款1.1升排量的Q型车、R型车的销量引起市场的关注.已知2010年1月Q型车的销量为a辆,通过分析预测,若以2010年1月为第1月,其后两年内Q型车每月的销量都将以1%的比率增长,而R型车前n个月的销售总量Tn大致满足关系式:Tn=228a(1.012n-1).(n≤24,n∈N*)
(1)求Q型车前n个月的销售总量Sn的表达式;
(2)比较两款车前n个月的销售总量Sn与Tn的大小关系;
(3)试问从第几个月开始Q型车的月销售量小于R型车月销售量的20%,并说明理由.
(参考数据:≈1.09,≈8.66)
查看习题详情和答案>>
(本小题满分12分)
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
(1)分别写出两种产品的收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
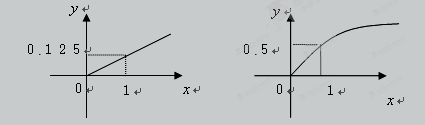
查看习题详情和答案>>
(本小题满分14分)甲、乙两间商店购进同一种商品的价格均为每件30元,销售价均为每件50元.根据前5年的有关资料统计,甲商店这种商品的年需求量![]() 服从以下分布:
服从以下分布:
|
| 10 | 20 | 30 | 40 | 50 |
|
| 0.15 | 0.20 | 0.25 | 0.30 | 0.10 |
乙商店这种商品的年需求量![]() 服从二项分布
服从二项分布![]() .
.
若这种商品在一年内没有售完,则甲商店在一年后以每件25元的价格处理;乙商店一年后剩下的这种商品第1件按25元的价格处理,第2件按24元的价格处理,第3件按23元的价格处理,依此类推.今年甲、乙两间商店同时购进这种商品40件,根据前5年的销售情况,请你预测哪间商店的期望利润较大?
查看习题详情和答案>>(本小题满分12分)某企业2005年的利润为500万元,因设备老化等原因,若不进行技术改造,预计企业利润将从2006年开始每年减少20万元。为此企业在2006年一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第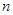 年利润为
年利润为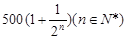 万元。
万元。
(1)若不进行技术改造,则从2006年起的前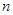 年的利润共
年的利润共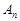 万元;若进行技术改造后,则从2006年起的前
万元;若进行技术改造后,则从2006年起的前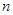 年的纯利润(扣除技术改造600万元资金)共
年的纯利润(扣除技术改造600万元资金)共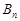 万元,分别求
万元,分别求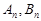 ;
;
(2)依据预测,从2006年起至少经过多少年技术改造后的纯利润超过不改造的利润?
查看习题详情和答案>>
(本小题满分14分)
某公司2009年9月投资14400万元购得上海世界博览会某种纪念品的专利权及生产设备,生产周期为一年.已知生产每件纪念品还需要材料等其它费用20元,为保证有一定的利润,公司决定纪念品的销售单价不低于150元,进一步的市场调研还发现:该纪念品的销售单价定在150元到250元之间较为合理(含150元及250元).并且当销售单价定为150元时,预测年销售量为150万件;当销售单价超过150元但不超过200元时,预测每件纪念品的销售价格每增加1元,年销售量将减少1万件;当销售单价超过200元但不超过250元时,预测每件纪念品的销售价格每增加1元,年销售量将减少1.2万件.
根据市场调研结果,设该纪念品的销售单价为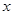 (元),年销售量为
(元),年销售量为 (万件),平均每件纪念品的利润为
(万件),平均每件纪念品的利润为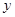 (元).
(元).
⑴求年销售量为 关于销售单价
关于销售单价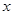 的函数关系式;
的函数关系式;
⑵该公司考虑到消费者的利益,决定销售单价不超过200元,问销售单价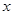 为多少时,平均每件纪念品的利润
为多少时,平均每件纪念品的利润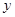 最大?
最大?
查看习题详情和答案>>