0 44967 44975 44981 44985 44991 44993 44997 45003 45005 45011 45017 45021 45023 45027 45033 45035 45041 45045 45047 45051 45053 45057 45059 45061 45062 45063 45065 45066 45067 45069 45071 45075 45077 45081 45083 45087 45093 45095 45101 45105 45107 45111 45117 45123 45125 45131 45135 45137 45143 45147 45153 45161 447348
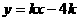 的图象与x轴交于点A,抛物线
的图象与x轴交于点A,抛物线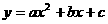 经过O、A两点。
经过O、A两点。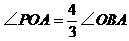 ?若存在,求出点P的坐标;若不存在,请说明理由。
?若存在,求出点P的坐标;若不存在,请说明理由。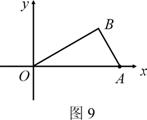


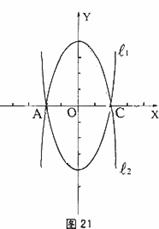
 的图象与x轴交于A、C两点。
的图象与x轴交于A、C两点。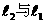 关于x轴对称,求
关于x轴对称,求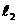 的解析式;(3分)
的解析式;(3分)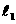 上一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点记为D,求证:点D在
上一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点记为D,求证:点D在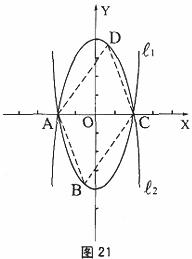
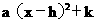 .
.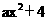 .
∴0=4a+4 得a=-1,
.
∴0=4a+4 得a=-1,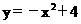 .
.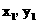 ) ∵点B在
) ∵点B在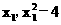 )
) 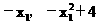 ).
). 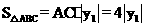 .
.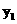 >0,
>0,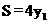 ,它是关于
,它是关于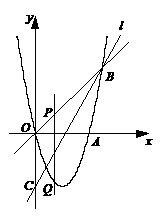 ∴S既无最大值也无最小值。
∴S既无最大值也无最小值。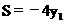 ,它是关于
,它是关于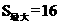 .
. 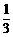 时,求直线DE的函数表达式;
时,求直线DE的函数表达式;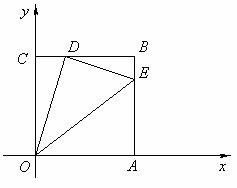
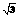 ,0),点M在⊙C上,并且∠BMO=120º。
,0),点M在⊙C上,并且∠BMO=120º。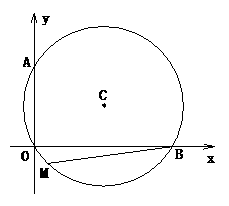
 的坐标为(-4,0),以点
的坐标为(-4,0),以点 (13,5)为圆心的圆与x轴相切于点D.
(13,5)为圆心的圆与x轴相切于点D. 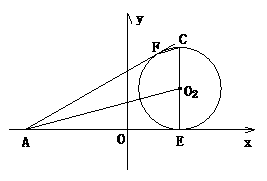
 ,AC = 6,BC =
8,点O在CB上,且AO平分∠BAC,CO = 3(如图所示),以点O为圆心,
,AC = 6,BC =
8,点O在CB上,且AO平分∠BAC,CO = 3(如图所示),以点O为圆心, 为半径画圆;
为半径画圆;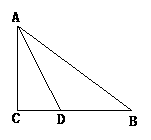
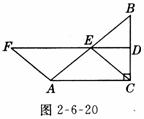 ⑶ 四边形ACEF有可能是正方形吗?为什么?
⑶ 四边形ACEF有可能是正方形吗?为什么?