3、(2005年潜江、仙桃、江汉油田)我们做一个拼图游戏:用等腰直角三角形拼正方形。请按下面规则与程序操作:
第一次:将两个全等的等腰直角三角形拼成一个正方形;

 第二次:在前一个正方形的四条边上再拼上四个全等的等腰直角三角形(等腰直角三角形的斜边与正方形的边长相等),形成一个新的正方形;
第二次:在前一个正方形的四条边上再拼上四个全等的等腰直角三角形(等腰直角三角形的斜边与正方形的边长相等),形成一个新的正方形;
以后每次都重复第二次的操作-------
(1)请你在第一次拼成的正方形的基础上,画出第二次和第三次拼成的正方形图形;
(2)若第一次拼成的正方形的边长为a,请你根据操作过程中的观察与思考填写下表:
|
操作次数(n) |
1 |
2 |
3 |
4 |
--- |
n |
|
每次拼成的正方形面积(s) |
a2 |
|
|
|
--- |
|
1、(包头)已知一次函数y1=x,二次函数y2=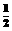 x2+
x2+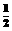 。
。
(1)根据表中给出的x的值,填写表中空白处的值;(2分)
|
x |
―3 |
―2 |
―1 |
0 |
1 |
2 |
3 |
|
y1=x |
―3 |
―2 |
―1 |
0 |
1 |
2 |
3 |
y2=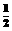 x2+ x2+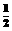 |
|
|
1 |
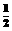 |
1 |
|
|
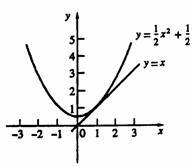 (2)观察上述表格中的数据,对于x的同一个值,判断yl和y2的大小关系。并证明:在实数范围内,对于x的同一个值,这两个函数所对应的函数值y1和y2的大小关系仍然成立;
(2)观察上述表格中的数据,对于x的同一个值,判断yl和y2的大小关系。并证明:在实数范围内,对于x的同一个值,这两个函数所对应的函数值y1和y2的大小关系仍然成立;
(3)若把y1=x换成与它平行的直线y=x+k(k为任意非零实数),请进一步探究:当k满足什么条件时,(2)中的结论仍然成立;当k满足什么条件时,(2)中的结论不能对任意的实数x都成立,并确定使(2)中的结论不成立的x的范围。
 对于边长为a的两个正方形ABCD和EFGH,按图1所示的方式摆放,在沿虚线BD,EG剪开后,可以按图中所示的移动方式拼接为图1中的四边形BNED。
对于边长为a的两个正方形ABCD和EFGH,按图1所示的方式摆放,在沿虚线BD,EG剪开后,可以按图中所示的移动方式拼接为图1中的四边形BNED。 请你参照图①,在图②中画出异于图①的一种图形,使夹在平行直线a和b之间的两条线段相等。
请你参照图①,在图②中画出异于图①的一种图形,使夹在平行直线a和b之间的两条线段相等。


 轴于D点,过点D作DF⊥AE于点F.
轴于D点,过点D作DF⊥AE于点F. (3)小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.
(3)小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由. 的图象于C、D两点,直线OC交BD于点M,直线CD交y轴于点H,记点C、D的横坐标分别为
的图象于C、D两点,直线OC交BD于点M,直线CD交y轴于点H,记点C、D的横坐标分别为 ,点H的纵坐标为
,点H的纵坐标为 。
。 2 :3 ②
2 :3 ②
 ”,其他条件不娈,结论①是否仍成立?
”,其他条件不娈,结论①是否仍成立? ,其他条件不娈,那么
,其他条件不娈,那么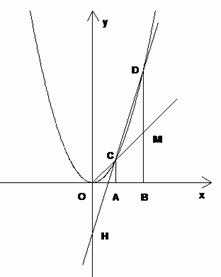
 经过坐标原点O,分别与x轴正半轴、y轴正半轴交于点A、B。
经过坐标原点O,分别与x轴正半轴、y轴正半轴交于点A、B。 ,求直线AC的解析式;
,求直线AC的解析式; 的内切圆的直径为d,试判断d+AB的值是否会发生变化,如果不变,求出其值,如果变化,求其变化的范围。
的内切圆的直径为d,试判断d+AB的值是否会发生变化,如果不变,求出其值,如果变化,求其变化的范围。


 处,两直角边分别与
处,两直角边分别与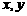 轴平行,纸板的另两个顶点
轴平行,纸板的另两个顶点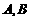 恰好是直线
恰好是直线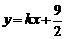 与双曲线
与双曲线 的交点.
的交点. (1)求
(1)求 和
和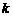 的值;
的值; ,让一把三角尺的直角顶点
,让一把三角尺的直角顶点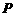 在
在 交于
交于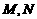 两点,请探究是否存在点
两点,请探究是否存在点 ,写出你的探究过程和结论.
,写出你的探究过程和结论. ∥
∥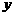 轴,
轴, ∥
∥ 轴,
轴,
 ,
, .
.

 或
或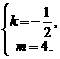
 且
且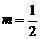 时,点A,B的坐标都是
时,点A,B的坐标都是 ,不合题意,应舍去;
,不合题意,应舍去; 且
且 时,点A,B的坐标分别为
时,点A,B的坐标分别为 ,
, ,符合题意.
,符合题意.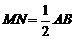 .
. ∥
∥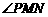
 ,∴Rt
,∴Rt ∽Rt
∽Rt ,∴
,∴ ,
, (1<x<8=,则M点坐标为
(1<x<8=,则M点坐标为 ,
, .又
.又 ,
, ,即
,即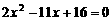 (※)
(※)  .∴方程(※)无实数根.
.∴方程(※)无实数根.
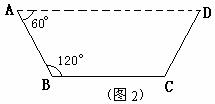 若∠ABC=120°,请你求出该水槽的横截面面积的最大值,并与方案①中的y的最大值比较大小.
若∠ABC=120°,请你求出该水槽的横截面面积的最大值,并与方案①中的y的最大值比较大小.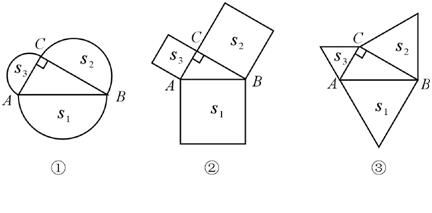
 ,得Rt△A
,得Rt△A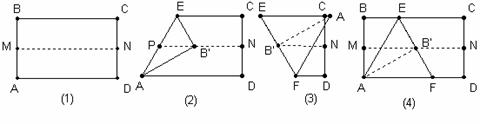
 =PM·PE=
=PM·PE= ,
,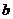 =PN·PF=
=PN·PF=
 ,
,
 ∴
∴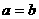

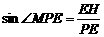



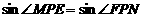
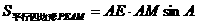 ,
,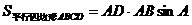
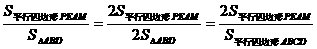

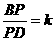 ,即
,即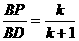 ,
,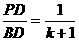 ,
,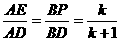 ,
,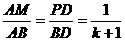
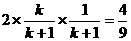 ,即
,即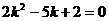 ∴
∴ ,
,
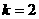 或
或 ,使得
,使得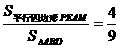 .
.