0 44924 44932 44938 44942 44948 44950 44954 44960 44962 44968 44974 44978 44980 44984 44990 44992 44998 45002 45004 45008 45010 45014 45016 45018 45019 45020 45022 45023 45024 45026 45028 45032 45034 45038 45040 45044 45050 45052 45058 45062 45064 45068 45074 45080 45082 45088 45092 45094 45100 45104 45110 45118 447348
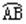 上任意一点,过E作⊙O的切线和PA、PB分别交于D、E,若OP=5,⊙O半径为3,则
上任意一点,过E作⊙O的切线和PA、PB分别交于D、E,若OP=5,⊙O半径为3,则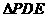 的周长为( )
的周长为( )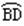 的度数为( )
的度数为( )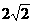 D.
D.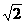
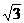 D.2
D.2 中,
中,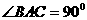 ,以AB为直径的⊙O交BC于点D,切线DE交AC于E。
,以AB为直径的⊙O交BC于点D,切线DE交AC于E。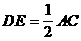
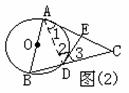
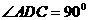 ,要证
,要证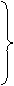 证明:连结AD
证明:连结AD
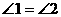
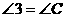
 AB为⊙O的直径Þ
AB为⊙O的直径Þ Þ
Þ 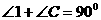
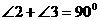
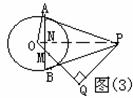
 PA、PB是⊙O的切线Þ PA=PB ÞOP⊥AB
PA、PB是⊙O的切线Þ PA=PB ÞOP⊥AB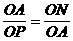 ÞOA2=OP·ON
ÞOA2=OP·ON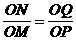 ÞON·OP=OM·OQ
ÞON·OP=OM·OQ  ,求CE、CD的长。
,求CE、CD的长。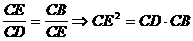 ;
;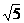 ÞCE=
ÞCE=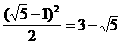
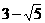 )
)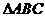 的外接圆,
的外接圆, 的平分线CE交AB于D,交⊙O于E,⊙O的切线EF交CB的延长线于F。
的平分线CE交AB于D,交⊙O于E,⊙O的切线EF交CB的延长线于F。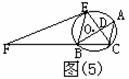

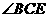 可得:AE=BE,所以,要证AE2=AD·EF,只需证
可得:AE=BE,所以,要证AE2=AD·EF,只需证 ∽
∽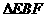
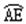 =
=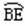 ÞAE=BE
ÞAE=BE
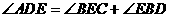
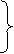
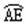 =
=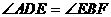
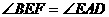
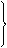 Þ
Þ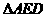 ∽
∽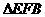 Þ
Þ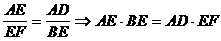 ÞAE2=AD·EF
ÞAE2=AD·EF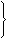 在⊙O1中:AC·CD=MC·NC ÞAC·CD=EC·BC
在⊙O1中:AC·CD=MC·NC ÞAC·CD=EC·BC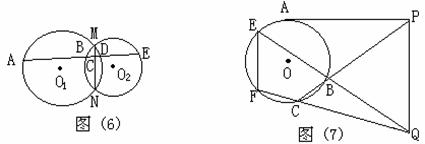
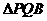 ∽
∽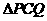 (2)PQ∥EF
(2)PQ∥EF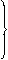
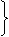 分析:有切线、割线,易联想到切割线定理,故有:AP2=PB·PC,因PQ=PA,所以PQ2=PB·PC,将此式改为比例式,再加上公共角∠BPQ,易证
分析:有切线、割线,易联想到切割线定理,故有:AP2=PB·PC,因PQ=PA,所以PQ2=PB·PC,将此式改为比例式,再加上公共角∠BPQ,易证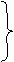
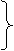 Þ
Þ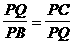 Þ△PBQ∽△PQCÞ∠PQB=∠PCQ
Þ△PBQ∽△PQCÞ∠PQB=∠PCQ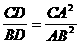
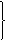 分析:由条件知:这是相似三角形的一种基本图形,易得△ADC∽△BDA,从而得:CA/AB=CD/AD=AD/DB,将此例式CA/AB=CD/AD (或
分析:由条件知:这是相似三角形的一种基本图形,易得△ADC∽△BDA,从而得:CA/AB=CD/AD=AD/DB,将此例式CA/AB=CD/AD (或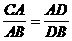 )两边平方,就符合结论的形式,再利用切割线定理的结论进行代换,命题就能得证。
)两边平方,就符合结论的形式,再利用切割线定理的结论进行代换,命题就能得证。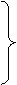 Þ
Þ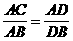 Þ
Þ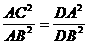
 AD为⊙O的切线 ÞAD2=DC·DB Þ
AD为⊙O的切线 ÞAD2=DC·DB Þ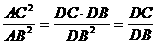 。
。