0 44926 44934 44940 44944 44950 44952 44956 44962 44964 44970 44976 44980 44982 44986 44992 44994 45000 45004 45006 45010 45012 45016 45018 45020 45021 45022 45024 45025 45026 45028 45030 45034 45036 45040 45042 45046 45052 45054 45060 45064 45066 45070 45076 45082 45084 45090 45094 45096 45102 45106 45112 45120 447348
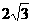 ,则圆心到该弦的距离是______.
,则圆心到该弦的距离是______. 如图:⊙O的直径AB⊥CD于P,
如图:⊙O的直径AB⊥CD于P, cm,l上一点P,PD=
cm,l上一点P,PD=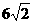 cm.⊙O的直径是20,则P在⊙O______.
cm.⊙O的直径是20,则P在⊙O______. (三)证明题:
(三)证明题: 求证:CD=2OO1
求证:CD=2OO1 此定理和三个推论的内容是平分弦,垂直弦是直径平分弧.在这四个条件中满足两个就可得到其它两个的结论.如垂直于弦是直径得到平分弦.平分弧(垂径定理)平分弦,是直径可得到垂直弦.平分弧(推论1)垂直弦,平分弦可得到这条直径是直径,且平分弦(推论2)
此定理和三个推论的内容是平分弦,垂直弦是直径平分弧.在这四个条件中满足两个就可得到其它两个的结论.如垂直于弦是直径得到平分弦.平分弧(垂径定理)平分弦,是直径可得到垂直弦.平分弧(推论1)垂直弦,平分弦可得到这条直径是直径,且平分弦(推论2) ∵AB是直径
∵AB是直径 由勾股定理得:OP=5cm OP=r ∴P在⊙O上
由勾股定理得:OP=5cm OP=r ∴P在⊙O上 ④弦:连结圆上位意两点的线段,
④弦:连结圆上位意两点的线段,
 ⑥弓形:由弦及其所对的弧组成的图形叫
⑥弓形:由弦及其所对的弧组成的图形叫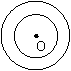 ⑧能够重合(或半径相等)的两个圆是等圆.
⑧能够重合(或半径相等)的两个圆是等圆.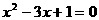 的两个根,两圆的圆心距为d,
的两个根,两圆的圆心距为d, ,
,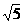 <d<3
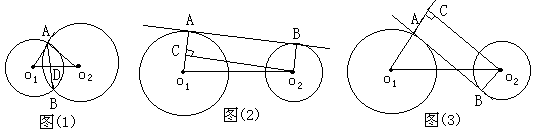
<d<3 AC为⊙o1的直径
AC为⊙o1的直径





 中,
中,


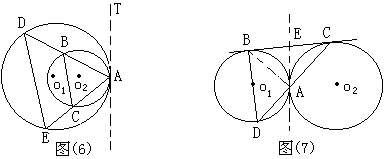
 ,所以只需证
,所以只需证 ,联想到两圆相交时常添的辅助线,再运用弦切角定理及圆内接四边形性质,问题易得证。
,联想到两圆相交时常添的辅助线,再运用弦切角定理及圆内接四边形性质,问题易得证。 CD切⊙o1于C
CD切⊙o1于C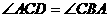

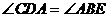


 成立吗?
成立吗?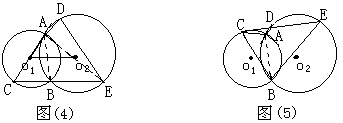
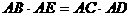
 ,即要证BC∥DE;
,即要证BC∥DE;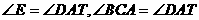
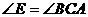 ∴BC∥DE
∴BC∥DE

 EB、EA为⊙o1的切线
EB、EA为⊙o1的切线
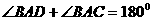
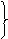
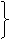



 ∽
∽

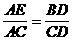 ,即要证
,即要证 ∽
∽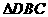 ,因两圆内切,所以可过点C作
,因两圆内切,所以可过点C作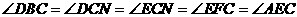
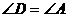 ,从而问题得以解决。
,从而问题得以解决。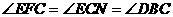

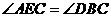


 中:
中: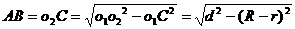
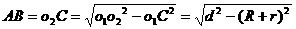


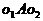 中,可以利用三角形有关知识加以解决。
中,可以利用三角形有关知识加以解决。