0 44714 44722 44728 44732 44738 44740 44744 44750 44752 44758 44764 44768 44770 44774 44780 44782 44788 44792 44794 44798 44800 44804 44806 44808 44809 44810 44812 44813 44814 44816 44818 44822 44824 44828 44830 44834 44840 44842 44848 44852 44854 44858 44864 44870 44872 44878 44882 44884 44890 44894 44900 44908 447348

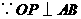
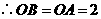 ······································································ 1分
······································································ 1分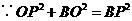
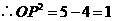 ,
,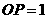 ······································· 2分
······································· 2分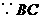 是
是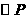 的直径
的直径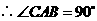 (也可用勾股定理求得下面的结论)
(也可用勾股定理求得下面的结论)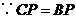 ,
,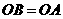
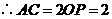 ················································· 3分
················································· 3分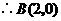 ,
,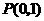 ,
,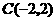 (写错一个不扣分)········································ 4分
(写错一个不扣分)········································ 4分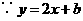 过
过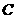 点
点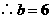
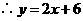 ·········································· 5分
·········································· 5分 当
当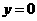 时,
时,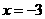
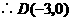

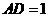 ··········································· 6分
··········································· 6分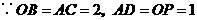 ,
,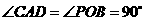
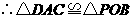
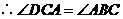
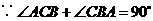
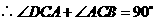 (也可用勾股定理逆定理证明)······························· 7分
(也可用勾股定理逆定理证明)······························· 7分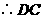 是
是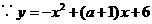 过
过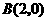 点
点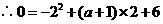
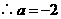 ···························································· 9分
···························································· 9分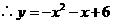 ························································································· 10分
························································································· 10分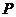 在
在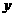 轴上,
轴上,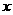 轴于
轴于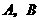 两点,连结
两点,连结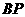 并延长交
并延长交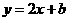 交
交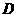 ,且
,且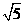 ,
,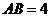 .
.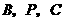 的坐标;
的坐标; 是
是 (3)若二次函数
(3)若二次函数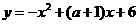 的图象经过点
的图象经过点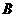 ,求这个二次函数的解析式,并写出使二次函数值小于一次函数
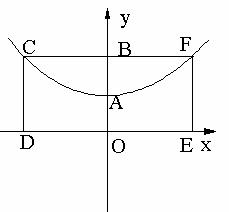
,求这个二次函数的解析式,并写出使二次函数值小于一次函数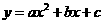 .其过三点A(0,1),C(-2.2),F(2,2)。
.其过三点A(0,1),C(-2.2),F(2,2)。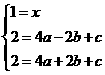 解这个方程组,得
解这个方程组,得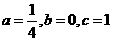
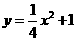 ………… (3分)
………… (3分)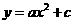 。 其过点A(0,1)和C(-2.2)
。 其过点A(0,1)和C(-2.2)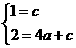 ……… 解这个方程组,得
……… 解这个方程组,得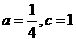
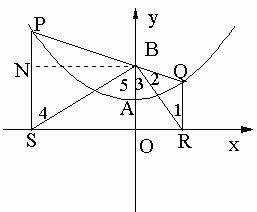
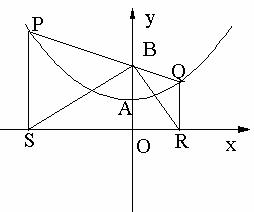
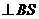 ,垂足为N.
,垂足为N.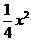 十l上.可设P点坐标为
十l上.可设P点坐标为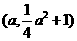 .
.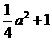 ,OB=NS=2,BN=
,OB=NS=2,BN=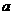 。
。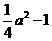 ………………………… (5分)
………………………… (5分)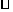 PNB中.
PNB中.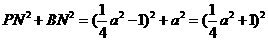
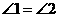 ,
,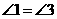 ,
,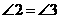 ,
,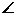 SBP=
SBP=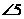 ………………………… (7分)
………………………… (7分)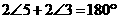
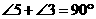
 .
.
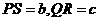 ,
,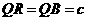 ,
,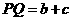 。
。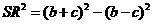
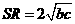 。………………………… (9分)
。………………………… (9分)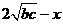 。
。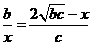 。
。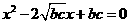
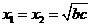 。
。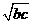
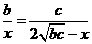 。
。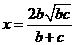 。
。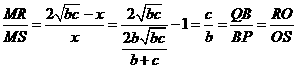 。
。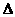 PSM∽
PSM∽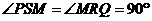 ,
,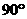 。
。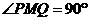 。………………………… (9分)
。………………………… (9分)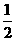 PQ=
PQ=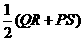 .……………… (10分)
.……………… (10分)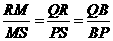
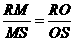 ,即M点与O点重合。
,即M点与O点重合。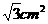 (2)等边三角形的边长a至少为10cm(3)等边三角形的边长为
(2)等边三角形的边长a至少为10cm(3)等边三角形的边长为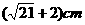
 上,NC=8cm。将直角梯形ABCD向左翻折180°,翻折一次得到图形①,翻折二次得图形②,如此翻折下去。
上,NC=8cm。将直角梯形ABCD向左翻折180°,翻折一次得到图形①,翻折二次得图形②,如此翻折下去。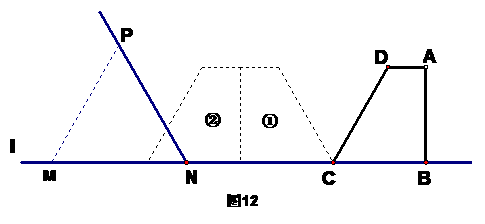
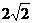 ,求t的值;
,求t的值;
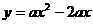 与直线
与直线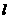 :
: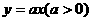 的交点除了原点
的交点除了原点 外,还相交于另一点
外,还相交于另一点 .
.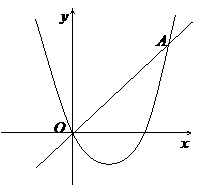 (1)分别求出这个抛物线的顶点、点
(1)分别求出这个抛物线的顶点、点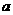 的式子表示);
的式子表示);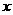 轴对折(翻转
轴对折(翻转 )后,得到的图象叫做“新抛物线”,则:
)后,得到的图象叫做“新抛物线”,则: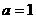 时,求这个“新抛物线”的解析式,并判断这个“新抛物线”的顶点是否在直线
时,求这个“新抛物线”的解析式,并判断这个“新抛物线”的顶点是否在直线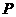 ,使点
,使点 的
的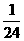 ?若存在,请直接写出满足条件的点
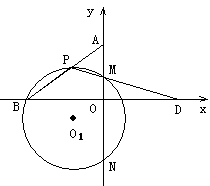
?若存在,请直接写出满足条件的点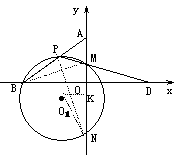 证明:作O1K⊥MN于K,连结O1N、PN、BM,
证明:作O1K⊥MN于K,连结O1N、PN、BM,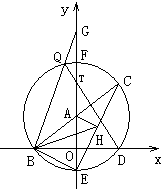 (3)如图2, P为线段AB上一动点(不与A、B两点重合),连结PD交y轴于点M,过P、M、B三点作⊙O1交y轴于另一点N,设⊙O1的半径为R,当k=时,给出下列两个结论:①MN的长度不变;②的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
(3)如图2, P为线段AB上一动点(不与A、B两点重合),连结PD交y轴于点M,过P、M、B三点作⊙O1交y轴于另一点N,设⊙O1的半径为R,当k=时,给出下列两个结论:①MN的长度不变;②的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.