摘要：已知:如图1.直线y=kx+3交x轴于点B.交y轴于点A.以A点为圆心.AB为半径作⊙A交x轴于另一点D.交y轴于点E.F两点.交直线AB于C点.连结BE.CF.∠CBD的平分线交CE于点H. (1)求证:BE=HE, (2)若AH⊥CE.Q为 上一点.连结DQ交y轴于T.连结BQ并延长交y轴于G. 求AT•AG的值, (3)如图2, P为线段AB上一动点.连结PD交y轴于点M.过P.M.B三点作⊙O1交y轴于另一点N.设⊙O1的半径为R.当k=时.给出下列两个结论:①MN的长度不变,②的值不变.其中有且只有一个结论是正确的.请你判断哪一个结论正确.证明正确的结论并求出其值.
网址：http://m.1010jiajiao.com/timu3_id_448111[举报]
已知：如图1，直线y=
x与双曲线y=
交于A，B两点，且点A的坐标为（6，m）．
（1）求双曲线y=
的解析式；
（2）点C（n，4）在双曲线y=
上，求△AOC的面积；
（3）过原点O作另一条直线l与双曲线y=
交于P，Q两点，且点P在第一象限．若由点A，P，B，Q为顶点组成的四边形的面积为20，请直接写出所有符合条件的点P的坐标．
查看习题详情和答案>>
| 1 |
| 3 |
| k |
| x |
（1）求双曲线y=
| k |
| x |
（2）点C（n，4）在双曲线y=
| k |
| x |
（3）过原点O作另一条直线l与双曲线y=
| k |
| x |
已知：如图，同一直线上有四点B、E、C、F，且 AB∥DE，AC∥DF，BE=CF．已知：如图1，直线AB∥CD，EF分别交AB、CD于E、F两点，∠BEF、∠DFE的平分线相交于点K．
（1）求∠EKF的度数．（计算过程不准用三角形内角和）
（2）如图2，∠BEK、∠DFK的平分线相交于点K1，问∠K1与∠K的度数是否存在某种特定的等量关系？写出结论并证明．
（3）在图2中作∠BEK1、∠DFK1的平分线相交于点K2，作∠BEK2、∠DFK2的平分线相交于点K3，依此类推，作∠BEKn、∠DFKn的平分线相交于点Kn+1，请用含的n式子表示∠Kn+1的度数．（直接写出答案，不必写解答过程）
查看习题详情和答案>>
（1）求∠EKF的度数．（计算过程不准用三角形内角和）
（2）如图2，∠BEK、∠DFK的平分线相交于点K1，问∠K1与∠K的度数是否存在某种特定的等量关系？写出结论并证明．
（3）在图2中作∠BEK1、∠DFK1的平分线相交于点K2，作∠BEK2、∠DFK2的平分线相交于点K3，依此类推，作∠BEKn、∠DFKn的平分线相交于点Kn+1，请用含的n式子表示∠Kn+1的度数．（直接写出答案，不必写解答过程）
探究规律：
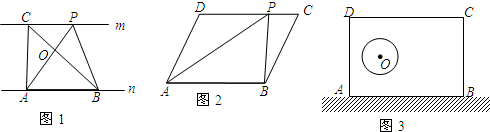
已知，如图1，直线m∥n，A、B为直线n上的两点，C、P为直线m上的两点．若A、B、C为三个定点，P为动点，则
（1）△PAB与△CAB的面积大小关系为 ；
（2）请你在图1中再画出一个与△ABC面积相等的△DEF，并说明面积相等的理由．
解决问题：
问题1：如图2，在?ABCD中，点P是CD上任意一点，
则S△PAB S△ADP+S△BCP（填写“＞”、“＜”或“=”）．
问题2：如图3，在公路旁边，有一块矩形的土地ABCD，其内部有一个底面为圆形的建筑物，点O为圆心．若要将土地（不含圆形建筑物所占的面积）平均分给两家承包，且分割线都过公路边（AB）上一点P，请你确定点P的位置，并画出分割线，说明理由．
查看习题详情和答案>>
已知，如图1，直线m∥n，A、B为直线n上的两点，C、P为直线m上的两点．若A、B、C为三个定点，P为动点，则
（1）△PAB与△CAB的面积大小关系为
（2）请你在图1中再画出一个与△ABC面积相等的△DEF，并说明面积相等的理由．
解决问题：
问题1：如图2，在?ABCD中，点P是CD上任意一点，
则S△PAB
问题2：如图3，在公路旁边，有一块矩形的土地ABCD，其内部有一个底面为圆形的建筑物，点O为圆心．若要将土地（不含圆形建筑物所占的面积）平均分给两家承包，且分割线都过公路边（AB）上一点P，请你确定点P的位置，并画出分割线，说明理由．
查看习题详情和答案>>
已知：如图，在直线MN上求作一点P，使点P到∠AOB两边的距离相等（要求写出作法，并保留作图痕迹，写出结论）