摘要:如图:直线y=x-2与x轴.y轴分别交于点A.B.M(t.0)是x轴上异于A的一点.以M为圆心且过点A的圆记为⊙M. (1)求证:直线AB将⊙M的周长分为1:3两部分, (2)若直线AB被⊙M所截得的弦长为.求t的值, (3)若点N是⊙M上的一点.是否存在实数t.使得四边形ABMN为平行四边形?若存在.求出t的值.并写出N的坐标,若不存在.说明理由.
网址:http://m.1010jiajiao.com/timu3_id_448114[举报]
 如图:直线
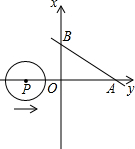
如图:直线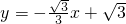 与x轴,y轴分别相交于A、B两点,半径为1的⊙P沿x轴向右移动,点P坐标为P(m,0),当⊙P与该直线相交时,m的取值范围是
与x轴,y轴分别相交于A、B两点,半径为1的⊙P沿x轴向右移动,点P坐标为P(m,0),当⊙P与该直线相交时,m的取值范围是
- A.-2≤m≤2
- B.1<m<5
- C.m>2
- D.1≤m≤5
 如图:直线y=-2x+5分别于x轴,y轴交于点C、D,与反比例函数y=
如图:直线y=-2x+5分别于x轴,y轴交于点C、D,与反比例函数y=| 3 |
| x |
①AD=BC;②EF∥AB;③四边形AEFC是平行四边形;④S△AOD=S△BOC,
其中正确的个数是( )
| A、1 | B、2 | C、3 | D、4 |
 如图:直线
如图:直线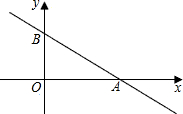 如图:直线y=kx+3与x轴、y轴分别交于A、B两点,
如图:直线y=kx+3与x轴、y轴分别交于A、B两点,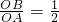 ,点C(x,y)是直线y=kx+3上与A、B不重合的动点.
,点C(x,y)是直线y=kx+3上与A、B不重合的动点.